Question

Is this asking whether or not the inequality is true? Or a value for f(x)?

Answer 1

`1 \leq x \leq 3`

Explanation:

The given graph shows function f(x).

To solve the given inequality, we must first determine the equation of the graphed function f(x).

Function f(x) is a straight line that intersects the y-axis at y = 6. Therefore, its y-intercept is 6. For every 1 unit increase along the horizontal direction, there is a corresponding decrease of 3 units along the vertical direction, which means that its slope is -3.

Substituting the slope (m) and y-intercept (b) into the slope-intercept form of a linear equation, y = mx + b, gives us the equation of function f(x):

`f(x)=-3x+6`

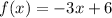
Substitute f(x) into the given inequality:

`-3 \leq -3x+6 \leq x+2`

To solve the compound inequality, break it down into its individual inequalities, solve each one separately, and then combine their solutions.

`\boxed{\textsf{If\;$a \leq u \leq b$,\;then\;$a\leq u$\;and\;$u\leq b$.}}`

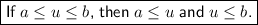
Inequality 1:

`\begin{aligned} -3 & \leq -3x + 6\\-3 -6& \leq -3x + 6-6\\-9 & \leq -3x\\-9 / -3 & \leq -3 / -3\\3 & \geq x\\x & \leq 3\end{aligned}`

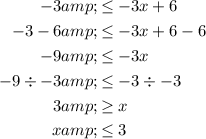
Inequality 2:

`\begin{aligned} -3x+6 &\leq x+2\\-3x+6-x &\leq x+2-x\\-4x+6&\leq2\\-4x+6-6&\leq2-6\\-4x&\leq-4\\-4x / -4 &\leq -4 / -4\\x&\geq 1\\\phantom{x}\end{aligned}`

Combine the intervals:

`1 \leq x \leq 3`

Therefore, the solution to the given inequality is:

`\large\boxed{1 \leq x \leq 3}`