Question

Find a value a > 0 so that the graph of the exponential function f(x) = aˣ contains the point (2,1/25).

a=

Answer 1

To find the value of 'a', we substitute the given point (2, 1/25) into the exponential function f(x) = aˣ and solve for 'a'. The value of 'a' is 1/5.

Step-by-step explanation:

To find the value of a that satisfies the equation, we can substitute the given point (2, 1/25) into the exponential function f(x) = aˣ. So, we have 1/25 = a². Taking the square root of both sides, we get a = 1/5.

Answer 2

A value of a that allows the graph of the given exponential function to contain the point (2, 1/25) include; a = 1/5.

In Mathematics and Geometry, an exponential function can be modeled by using this mathematical equation:

`f(x)=a(b)^x`

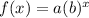
Where:

• a represents the initial value or y-intercept.
• x represents the time or x-variable.
• b represents the rate of change or common ratio.

Since the exponential function must contain the point (2, 1/25), we would substitute each of the coordinates of the point into the function as follows;

`f(x)=a^x\\\\(1)/(25) =a^2`

By taking the square root of both sides of the exponential function, we have the following:

`√(a^2) =\sqrt{(1)/(25) }`

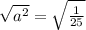
a = 1/5.