Question

Note: There will be some extra steps because the coefficient of x² is not 1. y = 3x²+ 30x + 68 Step 1: Separate non-x-terms from x-terms Step 2: Divide off the coefficient of x? Step 3: Identify the value that completes the square Step 4: Complete the Square y/3 -68 /3 x² + 10x Add 25 to both sides to complete the perfect square trinomial. y- 68/3 + 25 = x² + 10x + 25 Step 5: Factor and start solving for y

y/3+7/3=x²+10x+25
Factor the perfect square trinomial, and begin solving for y. y/3=
Step 6: Finish solving for y Step 7: Identify the vertex

Answer 1

Simplify the equation and write it as a perfect square.

Step-by-step explanation:

This is an equation in one variable, so we should be able to solve for the unknown value. This expression may look formidable, but first we can simplify the denominator and write it as a perfect square as well:

Answer 2

The vertex of the quadratic equation is (-5, -7).

Solving quadratic equation using completing the square.

The given quadratic equation y = 3x² + 30x + 68. The first step 1 was to separate non x-terms from x-terms. i.e.

y - 68 = 3x² + 30x

Step 2: Divide off the coefficient of x².

`(y)/(3)-(68)/(3)= (3x^2 )/(3) +(30x)/(3)`

`(y)/(3)-(68)/(3)= x^2 +10x`

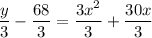
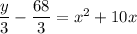
Step 3: Identify the value that completes the square.

Step 4: Complete the square:

`(y)/(3)-(68)/(3)= x^2 +10x`

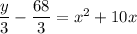
Add 25 to both sides to complete the perfect square trinomial;

`(y-68)/(3)+25= x^2 +10x + 25`

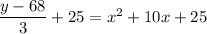
Step 5: Factor and start solving for y.

`(y)/(3)+(7)/(3) = x^2 +10x + 25`

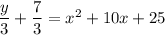
Factor the perfect square trinomial, and begin solving for y.

`(y)/(3)+(7)/(3) = (x + 5)^2`

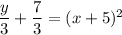
Step 6: Finish solving for y by multiplying both sides by 3.

y + 7 = 3(x + 5)²

Subtract 7 from both sides.

y = 3(x + 5)² - 7

Using the general formula for vertex y = a(x - h)² + k, so the vertex form for the quadratic equation is y = 3(x + 5)² - 7 and the vertex (h,k) is (-5, -7).