Question

A square picture frame has an outer perimeter of 28 and an inner perimeter of 20. What is the shortest distance between any two vertices?

Answer 1

Answer:
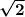`\boldsymbol{√(2)}` units

Step-by-step explanation:

Let square ABCD represent the outer perimeter, while EFGH is the smaller inside square.

The larger square has perimeter 28. The side length is 28/4 = 7 units.

We could have the following point locations

A = (0,0)

B = (7,0)

C = (7,7)

D = (0,7)

Refer to the diagram below.

Square EFGH has perimeter 20, so each side is 5 units long (because 20/4 = 5).

To recap, the smaller square has each side 5 units long, while the larger square has each side 7 units long.

The gap from 5 to 7 is 2 units, which splits in half to 2/2 = 1 unit. Therefore, the width of the frame is 1 unit.

Start at A = (0,0). Move 1 unit right and 1 unit up to get to E = (1,1)

Therefore we have these locations

E = (1,1)

F = (6,1)

G = (6,6)

H = (1,6)

Refer to the diagram below to notice that points A and E are one pair that are closest together. This will produce the shortest distance.

Use the distance formula to find the distance from A to E.

`(x_1,y_1) = (0,0) \text{ and } (x_2, y_2) = (1,1)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((0-1)^2 + (0-1)^2)\\\\d = √((-1)^2 + (-1)^2)\\\\d = √(1 + 1)\\\\d = √(2)\\\\d \approx 1.414214\\\\`

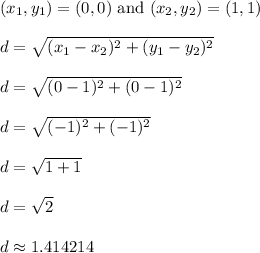
We could also select points G(6,6) and C(7,7)

`(x_1,y_1) = (6,6) \text{ and } (x_2, y_2) = (7,7)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((6-7)^2 + (6-7)^2)\\\\d = √((-1)^2 + (-1)^2)\\\\d = √(1 + 1)\\\\d = √(2)\\\\d \approx 1.414214\\\\`

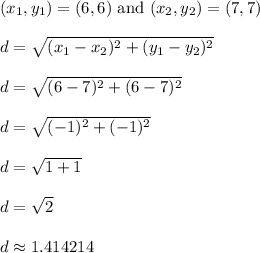
There are two other possible pairs we could have picked as well.

Therefore, the shortest distance between any two vertices is
`√(2)` units