Question

A polygon has n sides. Three of its interior angles are 50°, 60° and 70°.

The remaining (n – 3) exterior angles are each 15°. Calculate the value of n.

Answer 1

3

Explanation:

The sum of the exterior angles of a polygon is 360°.

Interior angles of 50°, 60°, and 70° corresponds to exterior angles of 130°, 120°, and 110°.

The remaining exterior angles are 15°.

Therefore:

130° + 120° + 110° + (n−3) × 15° = 360°

360° + (n−3) × 15° = 360°

(n−3) × 15° = 0

n−3 = 0

n = 3

Answer 2

Value of n is 3.

Explanation:

Given that:
The polygon has n sides, and three of its interior angles are 50°, 60° and 70°. with the remaining (n - 3) exterior angles each being 15°.

We know that the sum of the interior angles of a polygon with n sides can be calculated using the formula:

`\sf \textsf{Sum of interior angles} = (n - 2) * 180^\circ`

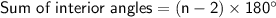
So, for this polygon:

`\sf 50^\circ + 60^\circ + 70^\circ + (n - 3) * 15^\circ = (n - 2) * 180^\circ`

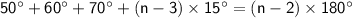
Simplify the equation:

`\sf 180^\circ + 15^\circ n - 45^\circ = 180^\circ n - 360^\circ`

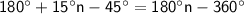
Combine like terms:

`\sf 15^\circ n - 45^\circ = 180^\circ n - 360^\circ`

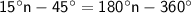
Subtract 15°n from both sides:

`\sf 15^\circ n - 45^\circ - 15^\circ n = 180^\circ n - 360^\circ - 15^\circ n`

`\sf -45^\circ = 165^\circ n - 360^\circ`

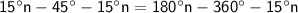
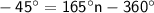
Add 360° to both sides:

`\sf \sf -45^\circ + 360^\circ = 165^\circ n - 360^\circ + 360^\circ`

`\sf 315^\circ = 165^\circ n`

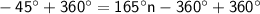
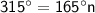
Divide by 165°.

`\sf n = (315^\circ)/(165^\circ)`

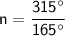
n = 3

Therefore, the value of n is 3, indicating that the polygon has 3 sides, which forms a triangle.