Question

Write the expression in standard form. (5+5i)(3-4i)

Answer 1

Hello :)

Answer:

35 - 5i

Explanation:

Our task is to simplify the expression:

`\sf{(5+5i)(3-4i)}`

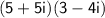
Use FOIL (First, outer, inner, last).

So, we multiply two complex numbers just like any two binomials.

First terms:

`\sf{5*3=15}`

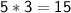
Outer terms:

`\sf{5*(-4i)=-20i}`

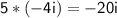
Inner terms:

`\sf{5i*3=15i}`

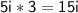
Last terms:

`\sf{5i*(-4i)=-20i^2}`

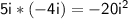
Combine like terms:

`\sf{15-20i+15i-20i^2}`

`\sf{15-5i-20i^2}`

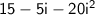
Also recall that i^2 = -1, so, we can simplify this even more, if we plug -1 for i^2, we can combine even more like terms, as follows:

`\sf{15-5i-20*(-1)}`

`\sf{15-5i+20}`

`\sf{-5i+20+15}`

`\sf{-5i+35}`

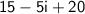
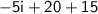
Write it in a + bi form:

`\implies\boxed{\sf{35-5i}}`

Answer 2

(5 + 5i)(3 - 4i) = 15 - 5i - 20i²

= 15 - 20(-1) - 5i

= 15 + 20 - 5i

= 35 - 5i