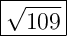Question

PLEASE HELP

Given z1 and z2, find the distance between them.
z1 = -20 + 17i and z2 = -10 + 14i
I can't figure it out and I keep making mistakes-

Answer 1

Given :

• z1 = -20+17i
• z2= -10+14i

To find :

• Distance between these two points.

Solution :

We know that ,

• 
  `d = \sqrt{(x_2 -x_1) {}^(2) + (y_2 -y_1) {}^(2) }`

Where,

• d = distance
• x2,x1 = co-ordinates of the first point
• y2,y1= co-ordinates of the second point

Though our points consist of variables ,we will consider their constant only to find out the distance.

Therefore,

• 
  `d = \sqrt{( - 10 - ( - 20)) {}^(2) + (14 - 17) {}^(2) } \\`
• 
  `d = \sqrt{ (- 10 + 20) {}^(2) + ( - 3) {}^(2) }`
• 
  `d = \sqrt{ {(10)}^(2) + ( - 3) {}^(2) }`
• 
  `d = √(100 + 9)`
• 
  `d = √(109)`
• 
  `d = 10.44`

Henceforth, The distance between z1 & z2 would be equal to 10.44 units .

Answer 2

`√(109)`

Explanation:

To find the distance between two complex numbers, use the following formula:

`\boxed{\begin{array}{l}\underline{\rm Distance\;between\;two\;complex\;numbers}\\\\d=√((a-x)^2+(b-y)^2)\\\\\\\sf Where\;the\;two\;complex\;numbers\;are\!:\\\\\phantom{ww}\bullet\;\;z_1=x+yi\\\phantom{ww}\bullet\;\;z_2=a+bi\\\\\end{array}}`

Given complex numbers:

`z_1=-20+17i \implies \boxed{x=20, y=17}`

`z_2=-10+14i \implies \boxed{a=-10, b=14}`

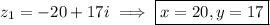
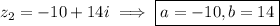
Substitute the values of x, y, a and b into the formula and solve for distance, d:

`\begin{aligned}d&=√((-10-(-20))^2+(14-17)^2)\\\\d&=√((10)^2+(-3)^2)\\\\d&=√(100+9)\\\\d&=√(109)\end{aligned}`

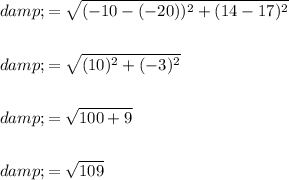
Therefore, the distance between the complex numbers z₁ and z₂ is:

`\Large\boxed{√(109)}`