Question

Consider the function f(x) 9-x^2/x^2-4. For which intervals is f(x) positive?

Answer 1

The function is increasing from
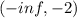`(-inf, -2)`U
`(-2, 0)`

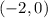
Explanation:

When viewing the equation (9-x^2)/(x^2-4), you may notice that the graph has two vertical asymptotes at x=-2 and x=2. This is because plugging in these values into the function will make those points undefined (divided by 0). Thus, you can assume that the graph is split into 3 separate sections that are (-inf, -2), (-2,2), and (2, inf). This question can be solved by testing points within those regions by plugging in values and watching the overall trend or by using derivatives.

By finding the first derivative, you will be left with
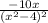`(-10x)/((x^2-4)^2)` = f'(x). By setting this point equal to 0, you will find that at x = 0, the slope of the function will be flat or equal to 0. This means that the function at x = 0 could either keep increasing or would begin to decrease. Thus, two separate possibilities could occur within the region of (-2, 2). You will likely need to test 4 separate regions.

Then, you can begin to plug in x-values into the first derivative equation within those 3 regions. If f'(x) = a positive integer, then the value is increasing. If f'(x) is negative, then the value is decreasing.

When testing x = -3, f'(x) is positive. The function is increasing from
`(-inf, -2)`

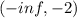
When testing x = -1, f'(x) is positive. The function is increasing from
`(-2, 0)`

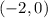
When testing x = 1, f'(x) is negative, the function is decreasing from
`(0, 2)`

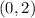
When testing x = 3, f'(x) is negative, the function is decreasing from
`(2, inf)`

Thus, the function is increasing from
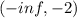`(-inf, -2)`U
`(-2, 0)`

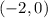
Hope this helps!