Question

ALERT!!!! PLEASE HELP MEEEEEEEE!!!! 50 PTS!!!!!

Answer 1

`\textsf{Period}=(23\pi)/(12)`

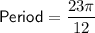
Explanation:

The period of a sinusoidal graph refers to the horizontal distance for which one complete cycle of the function occurs. In other words, the period is from one peak to the next (or from any point to the next matching point).

In the given graph, we can use the x-intercepts to calculate the period of the graphed function. One complete cycle of the function is from x = -3π/4 to x = 7π/6. Therefore, to find the period, calculate the difference between the two x-values:

`\textsf{Period}=(7\pi)/(6)-\left(-(3\pi)/(4)\right)`

`\textsf{Period}=(7\pi)/(6)+(3\pi)/(4)`

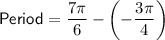
To add fractions, we need to have a common denominator. In this case, we have two fractions with different denominators, so we need to find a common denominator and then add the fractions together.

The least common multiple (LCM) of 6 and 4 is 12.

Therefore, convert both fractions to have a denominator of 12:

`\textsf{Period}=(7\pi)/(6)\cdot (2)/(2)+(3\pi)/(4)\cdot (3)/(3)`

`\textsf{Period}=(14\pi)/(12)+(9\pi)/(12)`

`\textsf{Apply the fraction rule} \quad (a)/(c)+(b)/(c)=(a+b)/(c):`

`\textsf{Period}=(14\pi+9\pi)/(12)`

`\textsf{Period}=(23\pi)/(12)`

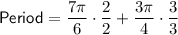
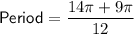
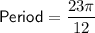
Therefore, the period of the graphed function is 23π/12.