Answer:
(a)
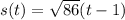
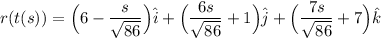
(b)
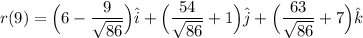
Explanation:
Given the vector function:

And the point:
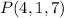

We need to find the arc length function s(t) for the curve measured from the point P in the direction of increasing t.
Part (a): Finding Arc Length Function.
The arc length of a curve is given by the integral of the magnitude of its derivative with respect to t. The derivative of the vector function r(t) is the velocity vector, and its magnitude is the speed of the particle moving along the curve.
Finding the velocity vector by taking the derivative of r(t):
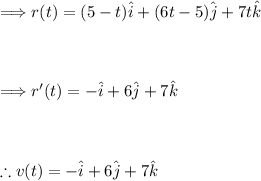
Now finding the magnitude of the velocity vector:
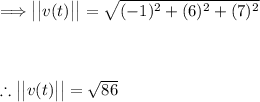
The arc length function, s(t), is the integral of the speed function with respect to t:

Where 'a' is a constant representing the starting point of the parameter.
Please be aware that the coordinates (4, 1, 7) correspond to t = 1. Hence, the arc length function is as follows:
![\Longrightarrow s(t) = \displaystyle \int\limits^t_1 {√(86) } \, du\\\\\\\\\Longrightarrow s(t) = \big[u√(86)\big]^t_1\\\\\\\\\Longrightarrow s(t) = \big[(t)√(86)-(1)√(86)\big]\\\\\\\\\Longrightarrow s(t)=t√(86)-√(86) \\\\\\\\\therefore \boxed{\boxed{s(t)=√(86)(t-1) }}](https://img.qammunity.org/2024/formulas/mathematics/college/h854som8ufatvddpvmm98kprahehuenut5.png)
Solving this integral, we find s(t) = √(86)(t - 1).
Now, we need to reparametrize the curve with respect to arc length starting from point P(4, 1, 7).
Let's denote the reparametrized curve as r(t(s)), where 't(s)' is the arc length function we found earlier. We need to find t(s).
From the equation s(t), we solve for t:
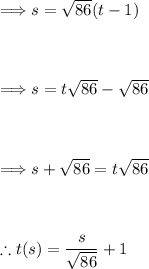
Substitute the value of t in the given curve:
![\text{Recall:} \ r(t) = (5-t)\hat i+(6t-5)\hat j + 7t\hat k\\\\\\\\\Longrightarrow r(s) = \Big(5-(s)/(√(86))+1\Big)\hat i+\Big(6\Big[(s)/(√(86))+1\Big]-5\Big)\hat j+7\Big((s)/(√(86))+1\Big)\hat k\\\\\\\\\therefore \boxed{\boxed{r(t(s))=\Big(6-(s)/(√(86))\Big)\hat i+\Big((6s)/(√(86))+1\Big)\hat j+\Big((7s)/(√(86))+7\Big)\hat k}}](https://img.qammunity.org/2024/formulas/mathematics/college/ylk5avpajp3odomxlyb8nw5rn8kmodgr98.png)

Part (b): Point 9 Units Along the Curve.
To find the point 9 units along the curve from P(4, 1, 7), we substitute s = 9 into the reparametrized curve equation:
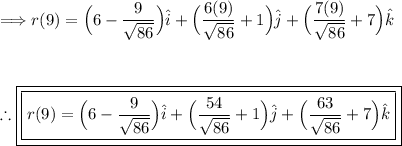
Thus, all parts have been solved.