Question

27. Rewrite the polar form of 12e9i

into a + bi form.
12e⁹i

Only need help with 27. Bless

Answer 1

`12\cos(9) + 12i\sin(9)\approx -10.934+4.945\:i`

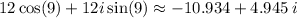
Explanation:

To rewrite the polar form of
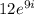`12e^(9i)` into a + bi form, where a and b are real numbers, we need to use Euler's formula:

`\large\boxed{e^(ix) = \cos(x) + i \sin(x)}`

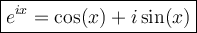
Here,
`i` is the imaginary unit, where
`i^2 = -1`, and the angle x is measured in radians.

For
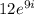`12e^(9i)`, x = 9. Therefore:

`12e^(9i) = 12 \left(\cos(9) + i \sin(9)\right)`

`12e^(9i) = 12\cos(9) + 12i\sin(9)`

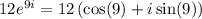
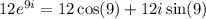
So, the expression
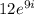`12e^(9i)` in a + bi form is:

`\large\boxed{12\cos(9) + 12i\sin(9)}`

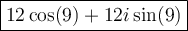
Evaluate 12cos(9) and 12sin(9):

`12\cos(9)=-10.93356314...=-10.934\;\sf(3\;d.p.)`

`12\sin(9)=4.94542182...=4.945\;\sf(3\;d.p.)`

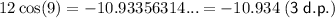
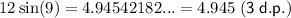
Therefore, the a + bi form of
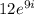`12e^(9i)` is approximately:

`\large\boxed{-10.934+4.945\:i}`