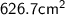Answer:
626.7 cm²
Explanation:
Given:
Middle one is rectangle.
Area of rectangle is given by: length* breadth
Area of rectangle = 30*15=450 cm^2
Again
if we join two half circle it will make a circle.
Area of two semi circle =

Here
Radius = 15/2 =7.5 cm
Now
aAre of two semi circle =

Now,
Total area = Area of rectangle + Area of two semi circle
Total Area

Total area =
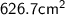
Therefore, the area of the polygon is