Question

!50 POINTS! (2 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1) b) 21 < d < 147

10) c) 9 m, 12 m, 15 m

Explanation:

Question 1

The Triangle Inequality Theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

In other words, if a, b, and c are the lengths of the sides of a triangle, then:

• a + b > c
• a + c > b
• b + c > a

From observation of the given diagram, the three side lengths of the triangle are:

• 63
• 84
• d

Using the Triangle Inequality Theorem, we can write the following inequalities:

`\begin{aligned}63 + 84& > d\\63 + d & > 84\\84 + d & > 63\end{aligned}`

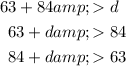
Solve each inequality for d:

`\begin{aligned}63+84& > d\\147& > d\\d& < 147\end{aligned}`

`\begin{aligned}63+d& > 84\\63+d-63& > 84-63\\d& > 21\end{aligned}`

`\begin{aligned}84+d& > 63\\84+d-84& > 63-84\\d& > -21\end{aligned}`

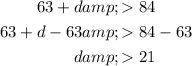
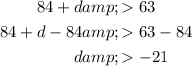
The first inequality tells us that d should be less than 147 yards.

The second inequality tells us that the d should be greater than 21 yards.

The third inequality tells us that d should be greater than zero (since length cannot be negative).

To find the possible values of d that satisfy all three inequalities, we need to consider the intersection of the solutions for each individual inequality.

Therefore, the possible values of d are:

• 21 < d < 147

`\hrulefill`

Question 10

Since triangle LMN is similar to triangle PQR, the ratios of corresponding side lengths must be equal.

The side lengths of triangle PQR are 3 cm, 4 cm and 5 cm.

Therefore, for triangle LMN to be similar to triangle PQR, its side lengths must be in the ratio 3k : 4k : 5k, where "k" is the scale factor.

When we take k = 300 (which means multiplying each side length of PQR by 300), we get the side lengths 900 cm, 1200 cm, and 1500 cm, which are equal to 9 m, 12 m and 15 m.

Therefore, the set of side lengths that could be those of triangle LMN are:

• 9 m, 12 m, 15 m