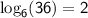Answer:
logarithmic form of
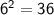 is
is
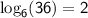
Explanation:
The general form for converting an exponential equation to logarithmic form is:

In this case, we have 6^2=36, so
b=6,
y=2, and
x=36.
Substituting these values into the general form, we get:
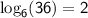
Therefore, the logarithmic form of
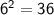 is
is