Question

If the first derivative of 57+42e^(-t/28) is -1.5e^(-t/28). What is f’(3)=-1.5e^(-t/28) ?

Answer 1

Answer: -1.5e^(-3/28), or -1.3476.

Explanation:

First of all, we need to determine in what term the derivative was taken so that we know what value should be substituted with 3 in the given derivative equation.

And if the derivative of 57 + 42e^(-t/28) is done in terms of t, using chain rule:

let,

`f(x) = 42e^(x)`

`f'(x) = 42e^(x)`

`g(x) = - (t)/(28)`

`g'(x) = - (1)/(28)`

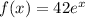
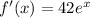
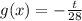
Then, f(g(x)) = 42e^(-t/28), our initial expression.

According to chain rule, because

d/dx f(g(x)) = f'(g(x))*g'(x),

when substituting,

we get 42e^(-t/28)*(-1/28)

= -1.5e^(-t/28).

which is the first derivative of 57+42e^(-t/28) given in the question.

Therefore, we can conclude that the derivative of 57 + 42e^(-t/28) in terms of t is equal to -1.5e^(-t/28), and in the given equation

f’(3)= -1.5e^(-t/28).

t = 3.

Simple Substituting, we get

-1.5e^(-3/28), or -1.3476.

Feel free to leave a comment if you have any question!