Question

Question 7(A) and question 7(B)

Answer 1

`7a.\ \mathrm{Solution:}\\\\(1)/(2+3i)=(2-3i)/((2+3i)(2-3i))=(2-3i)/(2^2-(3i)^2)=(2-3i)/(4+9)=(2)/(13)-(3)/(13)i`

`7b.\ \mathrm{Solution:}\\\\(5-i)/(-2+3i)=((5-i)(-2-3i))/((-2+3i)(-2-3i))=(-10-15i+2i+3i^2)/((-2)^2-(3i)^2)=(-10-13i-3)/(4+9)=(-13-13i)/(13)=-1-i`

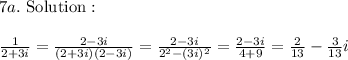
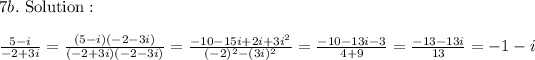
The trick here is to rationalize the expression. Rationalizing is the process of changing irrational denominator to rational or imaginary denominator to real. To do that, we simply multiply the denominator 'a+bi' with it's conjugate 'a-bi' to obtain a real number a^2+b^2.