Question

The drug reaction times (in minutes) for a sample of 12 random patients are given below:

{15, 9, 13, 14, 18, 8, 22, 20, 19, 25, 17 and 14}.
Which of the following values is the 1st Quartile (noted by Q1 on your TI device)?

Answer 1

13.5 minutes.

Explanation:

The first quartile (Q1) is the 25th percentile of the data.

This means that 25% of the data is lower than Q1 and 75% of the data is higher than Q1.

To calculate the first quartile, we first need to order the data from least to greatest:

8, 9, 13, 14, 14, 15, 17, 18, 19, 20, 22, 25

Since there are 12 data points.

Therefore, n = 12

we have

The formula for calculating the first quartile:

`\boxed{\sf Q_1 =\left(( (n ))/(4)\right)^(th)\textsf{ data point }}`

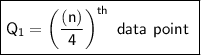
Where:

n = number of data points

substituting the value of n, we get

`\sf Q_1 =( (12)/(4) )^(th)=3 term`

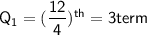
Q1 is the third data point.

However, since the third data point is 13, which is not the middle of the bottom 25% of the data, we need to average the third and fourth data points, which are 13 and 14.

`\sf Q1=((13 + 14))/(2 )= 13.5`

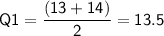
Therefore, Q1 is 13.5 minutes.

Answer 2

The 1st quartile (Q₁) of the given data set is 13.5.

Explanation:

To find the 1st quartile (Q₁) of a data set, begin by arranging the data in ascending order:

`\sf 8, 9, 13, 14, 14, 15, 17, 18, 19, 20, 22, 25`

To find the position of the lower quartile (Q₁), first work out n/4 (where n is the number of data values).

There are 12 data values in the given data set. Therefore, n = 12:

`(n)/(\sf 4)=\sf (12)/(4)=3`

As n/4 is a whole number, then the lower quartile is halfway between the values in this position and the position above. Therefore, Q₁ is halfway between the 3rd term (13) and the 4th term (14):

`\sf Q_1=(13+14)/(2)=13.5`

So, the 1st quartile (Q₁) of the given data set is 13.5.