Question

Find the solutions to the system of equations select all that apply.

Answer 1

C. (4, 5)

D. (0, -3)

`\hrulefill`

Explanation:

When two or more equations are graphed on the same coordinate system, the points where the curves intersect represent the solutions to the system of equations.

Therefore, the solutions to a given graphed system of equations are the points of intersection.

From inspection of the graph, it appears that the points of intersection are:

• (0, -3) and (4, 5)

To confirm this, solve the system of equations by the method of substitution.

Substitute the first equation into the second equation and rearrange to equal zero:

`\begin{aligned}x^2-2x-3&=2x-3\\x^2-2x&=2x\\x^2-2x-2x&=2x-2x\\x^2-4x&=0\\x(x-4)&=0\end{aligned}`

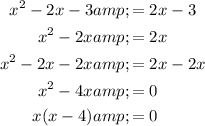
Solve for x:

`\begin{aligned}x&=0\implies x=0\\x-4&=0 \implies x=4\end{aligned}`

Substitute the found values of x into one of the equations to determine the y-values of the points of intersection:

`\begin{aligned}x=0 \implies y&=2(0)-3\\y&=-3\end{aligned}`

`\begin{aligned}x=4 \implies y&=2(4)-3\\y&=8-3\\y&=5\end{aligned}`

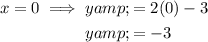
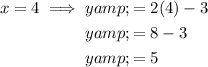
Therefore, this confirms that the solutions to the graphed system of equations are:

• C. (4, 5)
• D. (0, -3)

Answer 2

C. (4,5)

D. (0, -3)

Explanation:

Solutions of the system of equations are where they intersect.

We see they intersect at (4,5) and (0, -3), so the answer is C and D.