Question

If x^2 + y^2 =4x and dy/dt = 6, find dx/dt at the point (1, √3).

Answer 1

dx/dt = 6√3

Explanation:

To find dx/dt at the point (1, √3), we need to differentiate the given equation with respect to t and then solve for dx/dt when x = 1 and y = √3.

Given:

`x^2+y^2=4x`

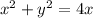
Step 1: Differentiate both sides of the equation with respect to t (time). Applying the chain rule.

`\Longrightarrow (d)/(dt) [x^2+y^2]=(d)/(dt) [4x]`

`\Longrightarrow 2x(dx)/(dt)+ 2y(dy)/(dt)=4(dx)/(dt)`

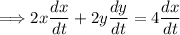
Step 2: Solve for dx/dt.

`\Longrightarrow 2y(dy)/(dt)=4(dx)/(dt)-2x(dx)/(dt)\\\\\\\\\Longrightarrow 2y(dy)/(dt)=(dx)/(dt)(4-2x)\\\\\\\\\therefore (dx)/(dt) = (2y\Big((dy)/(dt)\Big) )/(4-2x)`

Step 3: Substitute the values into the equation.

Given that dy/dt = 6 (from the problem statement), and we are looking for dx/dt at the point (1, √3), which means x = 1 and y = √3 at that point.

`\Longrightarrow (dx)/(dt) = (2y\Big((dy)/(dt)\Big) )/(4-2x)\\\\\\\\\Longrightarrow (dx)/(dt) = (2(\sqrt3)(6) )/(4-2(1))\\\\\\\\\Longrightarrow (dx)/(dt) = (12\sqrt3 )/(2)\\\\\\\\\therefore \boxed{ (dx)/(dt) = 6 \sqrt3}`

So, at the point (1, √3), dx/dt is equal to 6√3.

`\hrulefill`

Additional Information:

Implicit Differentiation: When we have an equation relating two or more variables, and each variable is a function of another variable (e.g., x and y are functions of t in this problem), we use implicit differentiation to find the derivatives of these variables with respect to the independent variable (t in this case). The chain rule is an essential tool in implicit differentiation.

Chain Rule: The chain rule is a fundamental concept in calculus that helps us find the derivative of a composite function. If we have a function f(g(x)), then the derivative of f(g(x)) with respect to x is given by:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Chain Rule:}}\\\\(d)/(dx)[f(g(x))]=f'(g(x)) \cdot g'(x) \end{array}\right }`

Derivative: The derivative of a function represents the rate of change of the function with respect to the independent variable. For example, dx/dt represents how the variable x is changing concerning time t.

Remember, when dealing with calculus problems, it's crucial to apply the chain rule and implicit differentiation correctly, and always pay attention to the points where you need to evaluate the derivatives.