Question

The surface area of a cube is 42 cm². What is the volume of the cube, rounded to the nearest tenth of a cm³?​

Answer 1

18.5 cm³

Explanation:

To find the volume of a cube with a surface area of 42 cm², we need to first calculate its side length. Since the surface area of a cube is given, we can use that information to find the side length and then calculate the volume.

The formula for the surface area of a cube is given by:

`\large\boxed{\sf Surface \;Area = 6 s^2}`

where "s" is the side length.

Given that the surface area is 42 cm², we can set up the equation using the formula, and solve for s:

`\begin{aligned}6s^2&=42\\\\(6s^2)/(6)&=(42)/(6)\\\\s^2&=7\\\\s&=√(7)\; \sf cm\end{aligned}`

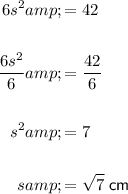
Now that we have the side length, we can calculate the volume of the cube.

The formula for the volume of a cube is given by:

`\large\boxed{\sf Volume = s^3}`

where "s" is the side length.

Substitute the found value of s into the formula for the volume of a cube:

`\begin{aligned}\sf Volume&=\left(√(7)\right)^3\\&=\left(√(7)\right)^2 \cdot \left(√(7)\right)^1\\&=7√(7)\\&=18.520259...\\&=18.5\; \sf cm^3\;(nearest\;tenth)\end{aligned}`

Therefore, the volume of the cube is 18.5 cm³, rounded to the nearest tenth.