Question

The equation for the circle below is x^2+y^2=25 what is the length of the circles radius

Answer 1

Answer : 5 units

Step by step Explanation:

Trust me bro I promise its right

Answer 2

5 units

Explanation:

The equation of a circle with center (h, k) and radius r is given by:

`\boxed{\sf (x - h)^2 + (y - k)^2 = r^2}`

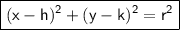
In the problem, the equation of the circle is given as:

`\sf x^2 + y^2 = 25`

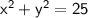
We can rewrite this equation as:

`\sf (x - 0)^2 + (y - 0)^2 = 5^2`

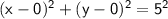
Comparing this equation to the standard form of the equation of a circle, we can see that the center of the circle is (0, 0) and the radius of the circle is 5.

Therefore, the length of the circle's radius is 5 units.