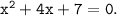Question

When solving a quadratic by completing the square, what value should be added to both sides of the equation x^2+4x+7=0?

Answer 1

Explanation:

The 'Expert' answer provided is INCORRECT....

To complete the square , the leading x^2 coefficient must be '1'....which for this example it already is.....

then you take 1/2 of the 'x' coefficient (1/2 *4 =2) and square it (2^2 = 4) and add the result to both sides of the equation

The answer to this question is '4'

To continue on to a solution ( not asked in the post )

x^2 + 4x + 4 + 7 = 4 '4' has been added to both sides of the equation

now reduce the L side

(x+2)^2 + 7 = 4 continue---- subtract 7 from both sides

(x+2)^2 = - 3

x+2 = ±sqrt -3

x = -2 ± sqrt(-3) = -2 - sqrt(3) i and -2 + sqrt (3) i

Answer 2

-3 should be added.

Explanation:

In order to solve the quadratic equation
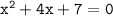`\tt x^2 + 4x + 7 = 0` by completing the square, you need to add a specific value to both sides of the equation in order to transform it into a perfect square trinomial.

Let's find the value should be added to both sides of the equation.

Given quadratic equation:

`\sf \sf x^2 + 4x + 7 = 0`

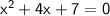
Comparing this equation with ax^2+bx+c = 0, we get b = 4.

Adding the value
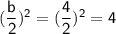`\sf ( (b)/(2))^2 =((4)/(2))^2=4` to both sides, where b is the coefficient of the linear term (4x).

The equation becomes:

`\sf x^2 + 4x + 4 + 7 = 4`

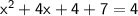
Factoring the perfect square trinomial on the left side and simplify the right side: using formula to factor :
`\boxed{\sf a^2 + 2ab+b^2 =(a+b)^2}`

`\sf (x + 2)^2 + 7 = 4`

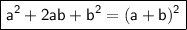
Isolating the squared term by subtracting both side by 7.

`\sf (x + 2)^2 = 4 - 7`

`\sf (x + 2)^2 = -3`

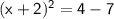
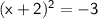
Since, we complete the perfect square in left hand side and the value that should be added to both sides of the equation is in right hand side.

Which means -3 should be added
`\tt x^2 + 4x + 7 = 0 .`