Question

Is the function represented by the table linear?

Answer 1

No, because it does not have a constant rate of change

Explanation:

for the table to represent a linear function then it must have a constant rate of change.

The rate of change can be found using the slope formula

m =
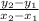`(y_(2)-y_(1) )/(x_(2)-x_(1) )` ( m represents slope )

consecutive ordered pairs from the table

(x₁, y₁ ) = (10,- 6 ) ) and (x₂, y₂ ) = (11, 1 )

m =
`(1-(-6))/(11-10)` =
`(1+6)/(1)` =
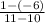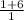`(7)/(1)` = 7

(x₁, y₁ ) = (12, 6 ) and (x₂, y₂ ) = (11, 1 )

m =
`(1-6)/(11-12)` =
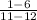`(-5)/(-1)` = 5

(x₁, y₁ ) = (13, 12 ) and (x₂, y₂ ) = (12, 6 )

m =
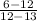`(6-12)/(12-13)` =
`(-6)/(-1)` = 6

As can be seen the values of m are not equal , then

the table does not represent a linear function