Question

For the following reaction, 21. 8 grams of iron are allowed to react with 45. 4 grams of chlorine gas.

iron ( s ) + chlorine ( g ) iron(III) chloride ( s )


What is the maximum amount of iron(III) chloride that can be formed? (grams)

What is the FORMULA for the limiting reagent?



What amount of the excess reagent remains after the reaction is complete?( grams)

Answer 1

To answer each of these questions, the first step you must complete is writing and balancing the correct chemical equation.

iron ( s ) + chlorine ( g ) iron(III) chloride ( s ) can also be written as:

Fe + Cl₂ ⇄ FeCl₃

which balanced is: 2Fe + 3Cl₂ ⇄ 2FeCl₃

After writing down your balanced equation, covert the grams you were given for iron and chlorine gas into moles using stoichiometry:

21.8 g Fe ×
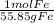`(1molFe)/(55.85gFe)` = 0.39 mol Fe

45.4 g Cl₂ ×
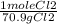`(1 mole Cl2)/(70.9 g Cl2)` = 0.64 mol Cl₂

Now that you have the moles of the reactants, you can figure of the limiting reactant using either stoichiometry or ICF.

This answer was solved using ICF

Now that you have your moles, set up an ICF chart. ICF means

initial - change = final

It should look like this:

2Fe + 3Cl₂ ⇄ 2FeCl₃

I. 0.39 mol 0.64 mol 0 mol

C. -2x -3x +2x

___________________________________________

F 0.39-2x 0.64-3x 2x

1. The first row of the table shows the initial amount of moles each substance started with. FeCl₃ started with 0 moles because it was not yet created when the reaction first started.
2. The second row represents the change that occurred during the reaction. This is determined by the coefficient placed in front of each element. Value is being subtracted from the reactants while FeCl₃ has an addition symbol because, during the reaction, amounts of each substance was taken away in order to create FeCl₃.
3. The last row is the final equation, representing initial - change = final [ICF]

Now, set the final equations for Fe and Cl₂ to zero and solve for x:

Fe: 0.39 - 2x = 0 Cl₂: 0.64 - 3x = 0

0.39 = 2x 0.64 = 3x

x = 0.195 x = 0.213

The lower number is the limiting reactant, so Fe is the limiting reactant.

*use x = 0.195 for the rest of the problem and ignore x = 0.213*

To find the maximum amount of FeCl₃ that is formed, plug in 0.195 into the final equation calculated in the ICF chart. (2x)

2 (0.195) = 0.39 mol FeCl₃

Now convert that into grams using stoichiometry:

0.39 mol FeCl₃ ×
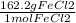`(162.2gFeCl2)/(1molFeCl2)` = 63.258 g FeCl₃

This is the maximum amount of FeCl₃ that can be formed

To calculate the amount of excess reactant/reagent after the reaction is complete, plug in 0.195 to the final equation for Cl₂ ( 0.64 - 3x)

0.64 - 3 (0.195)= 0.055 mol Cl₂

Convert this into grams using stoichiometry:

0.055 mol Cl₂ ×
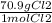`(70.9 gCl2)/(1 mol Cl2)` = 38.995 g Cl₂

This is the amount of excess reagent that remains once Fe is used up/reaches its limit