Question

Circle geometry help needed​

Answer 1

x = 40

Explanation:

the angles to the left and right at point B are a linear pair and sum to 180°

let the angle to the right be a , then

a + 50° = 180° ( subtract 50° from both sides )

a = 130°

the sum of the angles in a triangle = 180°

sum the 3 angles in the triangle with x

x + 10 + 130 = 180

x + 140 = 180 ( subtract 140 from both sides )

x = 40

Answer 2

x = 40

Explanation:

Circle Theorem vocabulary

• Secant: A straight line that intersects a circle at two points.
• Arc: The curve between two points on the circumference of a circle.
• Inscribed angle: The angle formed at the vertex when two chords intersect at a point on the circumference of a circle.
• Intercepted arc: The arc that is between the endpoints of the chords that form the inscribed angle.

The angles at the circumference subtended by the same arc are equal. Therefore, m∠KAB = 10°.

According to the Inscribed Angle Theorem, the measure of an inscribed angle is half the measure of the intercepted arc.

Inscribed angle ABD = 50°, so the minor intercepted arc DA = 100°.

Inscribed angle CDB = 10°, so the minor intercepted arc BC = 20°.

According to the Intersecting Secants Theorem, if two secant segments are drawn to the circle from one exterior point, the measure of the angle formed by the two lines is half of the (positive) difference of the measures of the intercepted arcs. Therefore:

`x^(\circ)=(1)/(2)\left(\overset{\frown}{DA}-\overset{\frown}{BC}\right)`

`x^(\circ)=(1)/(2)\left(100^(\circ)-20^(\circ)\right)`

`x^(\circ)=(1)/(2)\left(80^(\circ)\right)`

`x^(\circ)=40^(\circ)`

`x=40`

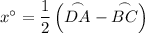
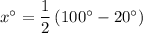
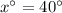
Therefore, the value of x is 40.