Question

Can someone please do the whole page ?? please !

(show work)

Answer 1

8.

A. o. S. = 0

Vetex = (0,3)

9.

A. o. S. = -1

Vetex = (-1,5)

10.
`\tt x \approx 16.45\textsf{ and }2.55`

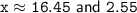
11. x = -6 and -2.

Explanation:

For question 8 and 9.

Note:

The axis of symmetry of a quadratic function is a vertical line that passes through the vertex of the parabola.

The vertex is the point on the parabola that is the highest (or lowest) point.

To find the axis of symmetry, we can use the formula
`\tt x = -(b)/(2a)`,

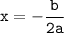where,

• a is the coefficient of the x² term.
• b is the coefficient of the x term.

To find the vertex, we can use the formula.
`\tt (-(b)/(2a), c)`,

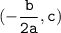where,

• c is the constant term.

For Question no. 8.

`\tt f(x) = -4x^2+3`

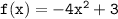
Comparing with
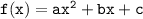`\tt f(x) = ax^2 + bx +c` we get,

a = -4 and b = 0 and c = 3

So, The axis of symmetry is
`\tt x = -(b)/(2a) = -(0)/(2*(-4)) = 0`

Now,

Vertex
`\tt (-(b)/(2a), c) = (0,3)`

`\hrulefill`

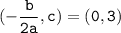
For Question no. 9.

`\tt f(x) = 3x^2-6x+5`

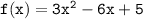
Comparing with
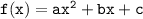`\tt f(x) = ax^2 + bx +c` we get,

a = 3 and b = -6 and c = 5

So, The axis of symmetry is
`\tt x = -(b)/(2a) = -(-6)/(2*(3)) = -1`

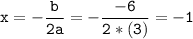
Now,

Vertex
`\tt (-(b)/(2a), c) = (-1,5)`

`\hrulefill`

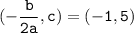
Solving the following equations.

The equations (x-4)(x-6)=0 and 2x(x-3)=0 can be solved by factoring the left side of each equation and setting each factor equal to 0.

10.) (x-4)(x-6)=0

The factors of (x-4)(x-6) are x-4 and x-6.

When we set each factor equal to 0, we get

(x-4)(x-6) = 0

either

x-4 = 0

x = 4

or

x-6 = 0

x = 6

Therefore, x = 4 or 6.

`\hrulefill`

11.) 2x(x-3)= 0

The factors of 2x(x-3) are 2x and x-3.

When we set each factor equal to 0, we get

2x(x-3) = 0

either

2x = 0

x = 0

or

x-3 = 0

x = 3

Therefore, x = 0 or 3.

`\hrulefill`

Let's solve question no. 12 by quadratic method and 13. by factorization method.

12.)
`x^2 - 19x + 42 = 0`

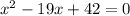
Comparing above equation with
`\tt ax^2 +bx +c =0`,

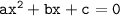we get

• a = 1
• b = -19
• c = 42

Using the quadratic formula:

`\boxed{\tt x = (-b \pm √(b^2 - 4ac))/(2a)}`

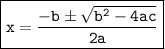
substituting value:

`\tt x = (-(-19) \pm √((-19)^2 - 4 \cdot 1 \cdot 42))/(2 \cdot 1)`

`\tt x = (19 \pm √(361 - 168))/(2)`

`\tt x = (19 \pm √(193))/(2)`

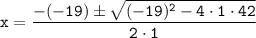
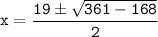
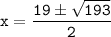
The two solutions for x are:

`\tt x = (19 + √(193))/(2) \approx 16.45`

`\ttx = (19 - √(193))/(2) \approx 2.55`

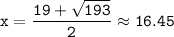
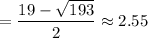
So, the values of x satisfying the quadratic equation are approximately 16.45 and 2.55

`\hrulefill`

13.

`\tt x^2 + 8x + 12 = 0`

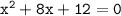
To factor the equation, we need to find two numbers that add up to 8 and multiply to 12. These numbers are 6 and 2.

We can rewrite the middle term using these two numbers:

`\tt x^2 +(6+2)x +12 =0`

`\tt x^2 + 6x + 2x + 12 = 0`

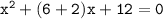
Taking common from each two terms

`\tt x(x+6)+2(x+6)=0`

Taking common and keeping remaining in another

`\tt (x+6)(x+2)=0`

It's Two solution are:

either

x + 6 = 0

x = -6

or

x + 2 = 0

x = -2

Therefore, the solutions to the equation are x = -6 and -2.