Question

A $525,000 adjustable rate mortgage is expected to have the following payments:

Year Interest Rate Monthly Payment
1–5 4% $2,506.43
6–15 6% $3,059.46
16–25 8% $3,464.78
26–30 10% $3,630.65


A fixed-rate mortgage in the same amount is offered with an interest rate of 4.65%.

What is the difference in the total cost between the two mortgages, rounded to the nearest dollar?

A spreadsheet was used to calculate the correct answer. Your answer may vary slightly depending on the technology used.

Answer 1

$176,580

Explanation:

To calculate the total cost difference between the two mortgages, we need to find the total payments made over the loan term for each mortgage and then subtract the total cost of the fixed-rate mortgage from the total cost of the adjustable-rate mortgage.

`\hrulefill`

Adjustable-rate mortgage

Calculate the payments made during each period of the adjustable-rate mortgage by multiplying the number of months in each period by the given monthly payment for each period.

Calculate the total cost of the adjustable-rate mortgage by summing the total payments per period:

`\begin{aligned}\sf Total\;cost&=\sf 150385.80 + 367135.20 + 415773.60 + 217839.00\\&=\sf 1151133.60\end{aligned}`

Therefore, the total cost of the adjustable-rate mortgage is:

• $1,151,133.60

`\hrulefill`

Fixed-rate mortgage

To find the total cost of the fixed-rate mortgage, calculate the monthly mortgage payment by using the monthly payment formula, then multiply this by the number of months in the term of the mortgage.

Monthly payment formula

`\boxed{\sf PMT=(Pi\left(1+i\right)^n)/(\left(1+i\right)^n-1)}`

where:

• PMT = Monthly payment.
• P = Loan amount.
• i = Interest rate per month (in decimal form).
• n = Term of the loan (in months).

Given values:

• P = $525,000
• i = 4.65%/12 = 0.0465/12 = 0.003875
• n = 30 years = 360 months

Therefore, the monthly payment (PMT) for the fixed-term mortgage is:

`\sf PMT=(525000(0.003875)\left(1+0.003875\right)^(360))/(\left(1+0.003875\right)^(306)-1)}`

`\sf PMT=(2034.375\left(1.003875\right)^(360))/(\left(1.003875\right)^(306)-1)}`

`\sf PMT=2707.09324...`

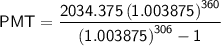
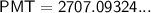
Multiply this by 360 months to calculate the total cost of the mortgage:

`\begin{aligned}\sf Total\;cost&=\sf PMT * 360\\&=\sf 2707.09324... * 360\\&= \sf 974553.567...\end{aligned}`

Therefore, the total cost of the fixed-rate mortgage is:

• $974,553.57

`\hrulefill`

Difference

To find the difference in total cost between the two mortgages, subtract the total cost of the fixed-rate mortgage from the total cost of the adjustable-rate mortgage:

`\begin{aligned} \sf Difference&= \sf \$1,151,133.60 - \$974,553.57\\&= \sf \$176,580.03\\&= \sf \$176,580\; (nearest\;dollar)\end{aligned}`

Therefore, the difference in the total cost between the two mortgages is $176,580, rounded to the nearest dollar.

This means that the fixed-rate mortgage is the better deal, as its total cost is $176,580 less than the adjustable-rate mortgage.