Answer:
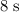 .
.
Step-by-step explanation:
To solve this question, start by finding the final velocity from the distance travelled in the last second of the motion. After that, divide the velocity gained during the entire motion by acceleration to find the duration of the motion.
Let
 be the final velocity.
be the final velocity.
The velocity at the beginning of the last second (
 ) would be
) would be
 , which is equal to
, which is equal to
 . Since acceleration is constant, average velocity in that period of
. Since acceleration is constant, average velocity in that period of
 would be:
would be:
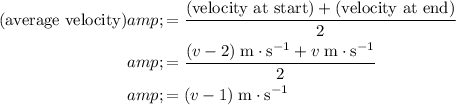 .
.
Multiply the average velocity by the duration to find an expression for the distance travelled within that
 :
:
 .
.
Given that the distance travelled in that period of time is
 :
:
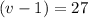 .
.
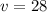 .
.
In other words, the final velocity of the person is
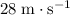 .
.
It is given that the initial velocity is
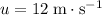 and acceleration is
and acceleration is
 .
.
In other words, velocity has increased from
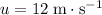 to
to
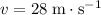 at a rate of
at a rate of
 . To find the time required, divide the change in velocity by the rate of change:
. To find the time required, divide the change in velocity by the rate of change:
 .
.
In other words, the time required was
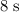 .
.