Question

\sqrt{3 - \sqrt{5} } + \sqrt{3 + \sqrt{5} }

Answer 1

`\sqrt{3 - √(5)} + \sqrt{3 + √(5)}=\boxed{√(10)}`

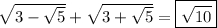
Explanation:

Given expression:

`\sqrt{3 - √(5)} + \sqrt{3 + √(5)}`

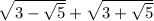
Set the expression equal to y (where y is the value of the expression).

`\sqrt{3 - √(5)} + \sqrt{3 + √(5)}=y`

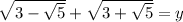
Square both sides:

`\left(\sqrt{3 - √(5)} + \sqrt{3 + √(5)}\right)^2=y^2`

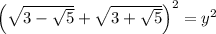
Apply the perfect square formula, (a + b)² = a² + 2ab + b², to the left side of the equation, where:

• 
  `a = \sqrt{3 - √(5)}`
• 
  `b = \sqrt{3 + √(5)}`

`\left(\sqrt{3 - √(5)}\right)^2 +2\left(\sqrt{3 - √(5)}\right) \left(\sqrt{3 + √(5)}\right)+\left(\sqrt{3 + √(5)}\right)^2=y^2`

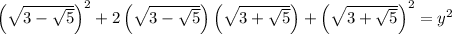
Evaluate the squared square roots:

`3 - √(5) +2\left(\sqrt{3 - √(5)}\right) \left(\sqrt{3 + √(5)}\right)+3 + √(5)=y^2`

`6+2\left(\sqrt{3 - √(5)}\right) \left(\sqrt{3 + √(5)}\right)=y^2`

`6+2\sqrt{3 - √(5)} \sqrt{3 + √(5)}=y^2`

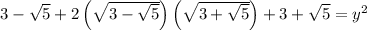
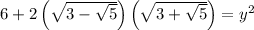
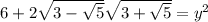
Apply the radical rule, √m√n = √(mn), and evaluate:

`\begin{aligned}6+2\sqrt{(3 - √(5))(3 + √(5))}&=y^2\\\\6 +2\sqrt{\left(9+3√(5)-3√(5)-5\right)} &=y^2\\\\6 +2√(4)& =y^2\\\\6 +2√(2^2) &=y^2\\\\6 +2(2) &=y^2\\\\6 +4 &=y^2\\\\10&=y^2\\\\√(10)&=√(y^2)\\\\√(10)&=y\\\\y&=√(10)\end{aligned}`

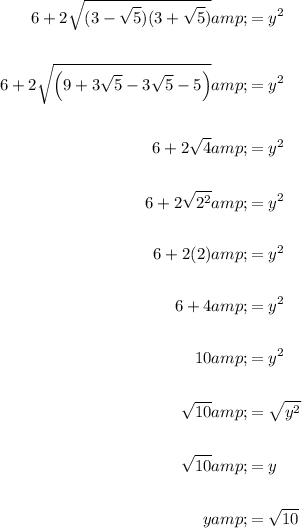
Therefore, the exact value of the expression is √(10).