A line's slope is the rate of change. It's calculated as:

But there's another formula for calculating the slope, and that is the slope formula:
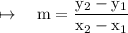
Where:
- m = slope
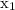 is the x-coordinate of the first point
is the x-coordinate of the first point
 is the x-coordinate of the second point
is the x-coordinate of the second point
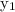 is the y-coordinate of the first point
is the y-coordinate of the first point
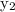 is the y-coordinate of the second point
is the y-coordinate of the second point
We can take any two points on the graph, plug them into the slope formula, and get the slope.
In this case, we're given the points (-3,4) and (2,-5), so we go ahead and substitute the values into the formula:
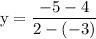
Simplify.
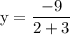
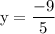
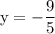
✦ Therefore, the slope is -9/5.
