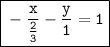Question

Write the slope-Intercept form of the given line. Include your work in your final answer. Type your answer in the box

provided to submit your solution.

Answer 1

`\textsf{Slope Intercept form}=\boxed{\tt -(x)/((2)/(3)) - (y)/(1) =1}`

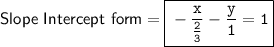
Explanation:

In order to find the slope-intercept form of the line, let's choose two points on the line.
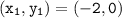`\tt (x_1,y_1)= (-2,0)` and
`\tt (x_2,y_2)= ( 0,-3).`

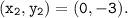
We can calculate the slope of the line using the following formula:

`\boxed{\boxed{\textsf{Slope(m) }\tt = ((y_2 - y_1))/((x_2 - x_1))}}`

Substitute the value, we get

`\tt m = (-3-0)/(0-(-2)) = -(3)/(2)`

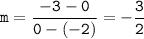
We have:

Equation of the line is given by the formula:

`\tt y-y_1 = m(x-x_1)`

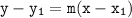
Taking one point
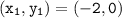`\tt (x_1,y_1)= (-2,0)` and substituting value, we get

`\tt y-0=-(3)/(2)(x-(-2))`

2y= -3(x+2)

2y = -3x -2

3x +2y = -2

Making it in the form of slope intercept form:
`\boxed{\tt (x)/(a)+(y)/(b)=1}`

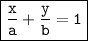
Dividing both side by -2, we get

`\tt (3x +2y )/(-2)=1`

`\tt -(x)/((2)/(3)) - y =1`

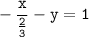
Therefore, The slope-Intercept form of the given line is
`\boxed{\tt -(x)/((2)/(3)) - (y)/(1) =1}`