Question

what is the perimeter of the shape with the given points A(-3,5) , B(2,6) , C(0,2) , and D(-5,1). answer choices: 22.8, 19.1, 12.4, 6.9​

Answer 1

* The points given are:

- A(-3,5)

- B(2,6)

- C(0,2)

- D(-5,1)

* To find the perimeter, we need to find the distance between each pair of consecutive points and add them up.

* The distances are:

- AB = sqrt((2-(-3))^2 + (6-5)^2) = sqrt(25 + 1) = 5

- BC = sqrt((0-2)^2 + (2-6)^2) = sqrt(4 + 16) = sqrt(20) = 4.47

- CD = sqrt((-5-0)^2 + (1-2)^2) = sqrt(25 + 1) = 5

- DA = sqrt((-3-(-5))^2 + (5-1)^2) = sqrt(16 + 16) = sqrt(32) = 5.66

* Adding these up:

- Perimeter = 5 + 4.47 + 5 + 5.66 = 20.13

So the perimeter is 20.13. Of the answer choices given, 19.1 is the closest. So the answer is 19.1.

Claude AI

Answer 2

19.1 units.

Explanation:

The perimeter of a shape is the total length of all its sides.

In this case, the shape is a quadrilateral, so we need to find the lengths of all four sides and add them up.

We can use the distance formula to find the length of each side. The distance formula is:

`\boxed{\tt d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)}`

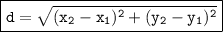
where d is the distance between the two points, x1 and y1 an are the coordinates of the first point, and x2 and y2 are the coordinates of the second point.

Here are the lengths of each sides of the quadrilateral, calculated using the distance formula:

`\tt AB = √((2-(-3))^2 + (6-5)^2)= √(25+1)=√(26)=5.099`

`\tt BC = √((0-2)^2 + (2-6)^2)= √(20) =2√(5)=4.47`

`\tt CD = √((-5 - 0)^2 + (1 - 2)^2) = √(26)=5.099`

`\tt DA = √((-3-(-5))^2 + (5 - 1)^2)=√(4+16)=√(20)=2√(5)=4.47`

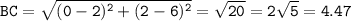
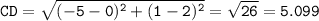
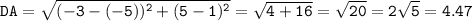
The perimeter of the quadrilateral is AB+BC+CD+DA

= 5.099 + 4.47 + 5.099 + 4.47 =19.13

Therefore, Perimeter of the shape is 19.1 units.