Answer:
Approximately
 .
.
Approximately
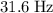 when mass is
when mass is
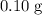 .
.
Step-by-step explanation:
Assume that the mass of the web is negligible, and that the insect is vibrating horizontally. Model the system of the vibrating insect and the web as a mass on a frictionless surface attached to a horizontal spring. Analyze the equations for a mass-spring system in simple harmonic motion to find the relationship between the spring constant, mass, and frequency.
In a frictionless horizontal mass-spring system, the net force on the mass is equal to the restoring force from the spring. When the mass is at a position of
 relative to the equilibrium position, the net force on the mass would be:
relative to the equilibrium position, the net force on the mass would be:
 .
.
(Negative because restoring force is opposite in direction to displacement.)
Acceleration of the mass
 would be:
would be:
 .
.
Let
 denote the spring constant, let
denote the spring constant, let
 denote the frequency of the motion, and let
denote the frequency of the motion, and let
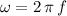 denote the angular velocity. In a simple harmonic motion, the acceleration
denote the angular velocity. In a simple harmonic motion, the acceleration
 and displacement
and displacement
 at time
at time
 can be modelled as:
can be modelled as:
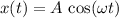 , and
, and
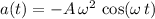 .
.
Where
 is the amplitude of the motion (
is the amplitude of the motion (
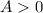 .)
.)
Since
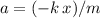 , substitute in the expression for
, substitute in the expression for
 and
and
 to obtain:
to obtain:
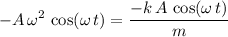 .
.
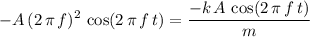 .
.
Simplify this expression (assuming that
 ) to obtain:
) to obtain:
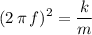 .
.
Solve for the spring constant
 :
:
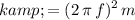 .
.
Apply unit conversion and ensure that mass is measured in standard units (kilograms):
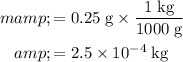 .
.
Given that
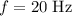 :
:
 .
.
In other words, the equivalent spring constant of the web is approximately
 .
.
In the other part of the question, the goal is to find frequency given mass
 (and that
(and that
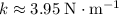 .) Rearrange the previous equation to find an expression for frequency
.) Rearrange the previous equation to find an expression for frequency
 in terms of mass
in terms of mass
 and spring constant
and spring constant
 :
:
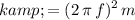 .
.
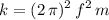 .
.
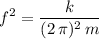 .
.
 .
.