Question

Last question. Finally. Please help one last time, PLEASE!

Answer 1

2. m∡1=80°

4. m∡2=100°

Only for specific triangle.

Explanation:

Statement (Reason in bracket)

1. m∡1+m∡A+m∡B=180°(The interior angle measures of a triangle sum to 180)

m∡1+60°+40°=180°

m∡1=180°-60°-40°

2. m∡1=80° (substituting value of m∡1)

3. m∡1+m∡2=180° (The angle measures of a linear pair sum to 180°)

80°+ m∡2=180°

m∡2=180°-80°

m∡2=100°

4. m∡2=100° (Substitute and solve for m∡2)

5. m∡A+m∡B = 100°( Add given angle measures)

6. m∡2=m∡A+ m∡C (Substitution)

Therefore, we proved the conclusion that it is true for this specific triangle only, since the angles of other triangles could be formed in a differently.

Therefore, we proof the conclusion for only for specific triangle.

`\boxed{\tt Good\: Luck}`

Answer 2

`\textsf{Statement\;2:} \quad m \angle 1 =\boxed{80^(\circ)}`

`\textsf{Statement\;4:} \quad m \angle 2 =\boxed{100^(\circ)}`

`\Large\textcircled{\small B}}\;\;\sf Only\; for\; this\; specific \;triangle`

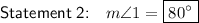
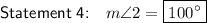
Explanation:

Statement 2

As the interior angles of a triangle sum to 180°, then for the given triangle we can say that:

`m \angle 1 + m \angle A + m \angle C = 180^(\circ)`

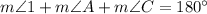
From inspection of the given triangle, m∠A = 60° and m∠C = 40°.

Substitute these angles into the equation from statement 1 and solve for m∠1:

`m \angle 1 + 60^(\circ) + 40^(\circ) = 180^(\circ)`

`m \angle 1 + 100^(\circ) = 180^(\circ)`

`m \angle 1 + 100^(\circ)-100^(\circ) = 180^(\circ)-100^(\circ)`

`m \angle 1 =80^(\circ)`

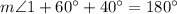
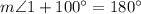
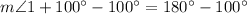
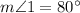
Therefore, the measure of angle 1 is 80°.

`\hrulefill`

Statement 4

A linear pair is two angles which when combined together form a straight line. Therefore, the angle measures of a linear pair sum to 180°.

As ∠1 and ∠2 form a linear pair, we can say that:

`m \angle 1 + m \angle 2= 180^(\circ)`

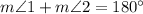
Substitute the found value of m∠1 and solve for m∠2:

`80^(\circ) + m \angle 2= 180^(\circ)`

`80^(\circ) + m \angle 2-80^(\circ)= 180^(\circ)-80^(\circ)`

`m \angle 2= 100^(\circ)`

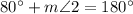
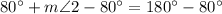
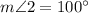
Therefore, the measure of angle 2 is 100°.

`\hrulefill`

The conclusion is only true for this specific triangle, since the angles of other triangles could be labelled in a different way.

For example, ∠A in this triangle could be labelled as ∠B in another triangle, which would mean that this specific conclusion would not hold true.