The volume of the given solid under the surface
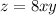 and above the triangle with vertices
and above the triangle with vertices
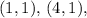 and
and
 is
is
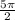 cubic units.
cubic units.
To find the volume of the solid under the surface, you can set up a triple integral using cylindrical coordinates. Here's the step-by-step process:
Step 1: Determine the limits of integration for
 ,
,
 , and
, and
 .
.
1.
 varies from 0 to the distance from the origin to the farthest point on the triangle, which is
varies from 0 to the distance from the origin to the farthest point on the triangle, which is
 .
.
2.
 can range from 0 to
can range from 0 to
 since we are working with the first quadrant.
since we are working with the first quadrant.
3.
 will vary from 0 to the height of the region, which is
will vary from 0 to the height of the region, which is
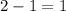 .
.
Step 2: Set up the triple integral for the volume:
![\[V = \iiint_E dV\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nfsee4lpar7vocb958iuhudua2is5acaeu.png)
Where
 is the region in cylindrical coordinates:
is the region in cylindrical coordinates:
![\[E = \{(r, \theta, z) : 0 \leq r \leq √(10), 0 \leq \theta \leq (\pi)/(2), 0 \leq z \leq 1\}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rkak6bzs27ts10tlb9w6aablvhuho49fqb.png)
So, the integral becomes:
![\[V = \int_0^{(\pi)/(2)} \int_0^(√(10)) \int_0^1 r \, dz \, dr \, d\theta\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4abn3ouu1lwml1dehptg298i08n26ezo7u.png)
Step 3: Evaluate the integral.
First, integrate with respect to
 :
:
![\[\int_0^1 r \, dz = r \cdot z \bigg|_0^1 = r\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6nv3ohxchrfzhjpxgn19cwkir9w2693nc0.png)
Now, we have:
![\[V = \int_0^{(\pi)/(2)} \int_0^(√(10)) r \, dr \, d\theta\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ih8ve8t6ezihb0arqxuofh6dv8vrpxssd4.png)
Next, integrate with respect to
 :
:
![\[\int_0^(√(10)) r \, dr = (1)/(2)r^2 \bigg|_0^(√(10)) = (1)/(2)(10) - (1)/(2)(0) = 5\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r5macua5glahwbvebp2oq8yqe1qgaon3g2.png)
Now, we have:
![\[V = \int_0^{(\pi)/(2)} 5 \, d\theta\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1o05wlozb1kue8sqzpv2dyal20enzi7f3a.png)
Finally, integrate with respect to
 :
:
![\[\int_0^{(\pi)/(2)} 5 \, d\theta = 5\theta \bigg|_0^{(\pi)/(2)} = 5\left((\pi)/(2)\right) - 5(0) = (5\pi)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/r9nwd52loaac3l15qty2ojgqmh6rczot40.png)
So, The answer is
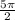 cubic units.
cubic units.