1. The vertical height
 of the slope is approximately 12.94 meters. Using the conservation of energy principle, the spring constant
of the slope is approximately 12.94 meters. Using the conservation of energy principle, the spring constant
 of the spring is calculated to be approximately
of the spring is calculated to be approximately
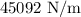 .
.
2. The correct option is c. Thermal energy.
The scenario described involves a physics problem where we need to find the spring constant of a spring that compresses a certain distance when impacted by a bobsled. The problem is a classic example of the conservation of mechanical energy, assuming no energy is lost due to non-conservative forces like friction or air resistance.
1. Here are the steps to solve the problem:
1. Identify the Initial and Final States: The initial state is the bobsled at rest at the top of the slope, and the final state is the bobsled compressed against the spring.
2. Calculate the Potential Energy at the Start: The gravitational potential energy at the start
 can be calculated using the formula
can be calculated using the formula
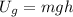 , where
, where
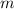 is the mass of the bobsled,
is the mass of the bobsled,
 is the acceleration due to gravity, and
is the acceleration due to gravity, and
 is the vertical height of the slope which can be found from the length of the slope
is the vertical height of the slope which can be found from the length of the slope
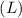 and the angle
and the angle
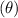 .
.
3. Calculate the Kinetic Energy Just Before Impact: As the bobsled slides down the slope, it converts potential energy into kinetic energy. Just before impact, all the potential energy will have been converted to kinetic energy
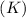 , which is given by
, which is given by
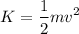 .
.
4. Apply the Conservation of Energy Principle: At the point of maximum compression, all the kinetic energy will have been converted into elastic potential energy stored in the spring
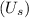 , which is given by
, which is given by
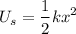 , where
, where
 is the spring constant, and
is the spring constant, and
 is the compression of the spring.
is the compression of the spring.
5. Set up the Equation and Solve for
 : Since energy is conserved,
: Since energy is conserved,
 at the start will be equal to
at the start will be equal to
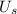 at the point of maximum compression. We can set up the equation
at the point of maximum compression. We can set up the equation
 and solve for
and solve for
 .
.
Calculations based on the given information:
- Mass of the bobsled,
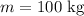
- Length of the slope,

- Angle of the slope,

- Compression of the spring,
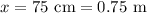
- Acceleration due to gravity,
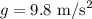
Let's find the height
 using the angle
using the angle
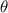 and the length
and the length
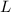 , and then calculate the spring constant
, and then calculate the spring constant
 .
.
1. The height $h$ from which the bobsled starts sliding is calculated using the sine component of the angle, which gives us
 meters.
meters.
2. Using the potential energy formula
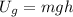 , we find the total potential energy at the top of the slope.
, we find the total potential energy at the top of the slope.
3. Knowing that this potential energy converts into elastic potential energy at maximum compression, we set the gravitational potential energy equal to the spring's elastic potential energy,
 .
.
4. Solving for
 gives us the spring constant, which is approximately
gives us the spring constant, which is approximately
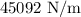 .
.
So, the spring constant of the spring is around
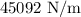 .
.
2. As the bobsled moves down the slope and hits the spring, the following types of energy change:
1. Gravitational Potential Energy: This decreases as the bobsled moves down the slope because the height with respect to the ground is decreasing.
2. Kinetic Energy: This increases as the bobsled moves down the slope because it is accelerating due to gravity and converting potential energy into kinetic energy.
3. Elastic Potential Energy: This increases only when the bobsled contacts and compresses the spring. Before contact with the spring, there is no elastic potential energy involved.
4. Thermal Energy: Although not explicitly stated in the problem, in a real-world scenario, thermal energy would increase due to friction between the bobsled and the slope, as well as within the spring as it compresses and then decompresses.
In a theoretical, ideal scenario where non-conservative forces like friction are ignored (which is often the case in physics problems unless otherwise stated), the only energies considered to change would be gravitational potential energy, kinetic energy, and elastic potential energy. However, if we consider a realistic scenario, then thermal energy would also increase due to frictional forces.
The complete question is here: