Question

An artifact is found in a desert cave. The anthropologists who found this artifact would like to know its age. They find that the present activity of the artifact is 9.25 decays/s and that the mass of carbon in the artifact is 0.100 kg. To find the age of the artifact, they will need to use the following constants: - r=1.2×10

−12
, - m
a
​
=2.32×10
−26
kg - λ=1.21×10
−4
year
−1
. What is the age of the artifact? Be mindful of the units. Express your answer in years to two significant figures.

Answer 1

The age of the artifact is approximately 7,054 years.

Step-by-step explanation:

To determine the age of the artifact, we can use the formula for radioactive decay:

`\[ N(t) = N_0 \cdot e^(-\lambda t) \]`

where N(t) is the present activity, N_0 is the initial activity,
`\(\lambda\)` is the decay constant, and t is the time in years. The initial activity N_0 is related to the mass of carbon m_a using the formula
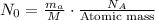`\(N_0 = (m_a)/(M) \cdot \frac{N_A}{\text{Atomic mass}}\)`, where M is the molar mass of carbon and N_A is Avogadro's number.

Given the present activity N(t) as 9.25 decays/s, the mass of carbon m_a as 0.100 kg, and the decay constant
`(\(\lambda\))` as 1.21 × 10^(-4) year^(-1), we can rearrange the decay equation to solve for t. Plugging in the values, we get:

`\[ 9.25 = (0.100)/(M) \cdot \frac{N_A}{\text{Atomic mass}} \cdot e^{-1.21 * 10^(-4) \cdot t} \]`

Solving for \(t\), we find the age of the artifact to be approximately 7,054 years.

In summary, the age of the artifact is determined by relating its present activity to the initial activity using the radioactive decay equation. The calculation involves the mass of carbon, Avogadro's number, and the decay constant. The final result, 7,054 years, provides an estimate of the artifact's age based on its radioactive decay.