The energy delivered to the
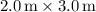 wall in 1.0 minute by the sound wave is approximately
wall in 1.0 minute by the sound wave is approximately
 .
.
To find the maximum displacement of the air molecules produced by the waves, we can use the relationship between sound pressure level (SPL) and maximum particle displacement
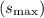 for a given frequency.
for a given frequency.
The formula relating sound pressure level to maximum displacement for infrasound is given by:
![\[ \text{SPL} = 20 \log_(10)\left(\frac{s_{\text{max}}}{\text{reference pressure}}\right) \]](https://img.qammunity.org/2024/formulas/physics/high-school/z2ljkj80y61nkhwumfet66zui6f40m6qbb.png)
Given:
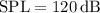
Frequency
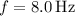
Reference pressure for sound in air
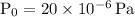 (standard reference pressure)
(standard reference pressure)
Let's solve for
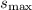 using the formula:
using the formula:
![\[120 = 20 \log_(10)\left(\frac{s_{\text{max}}}{20 * 10^(-6)}\right)\]](https://img.qammunity.org/2024/formulas/physics/high-school/zvy1b500ee0n2fjwbixeemjhuzfa43dzlq.png)
First, rearrange the equation to solve for

![\[\frac{s_{\text{max}}}{20 * 10^(-6)} = 10^((120 / 20))\]](https://img.qammunity.org/2024/formulas/physics/high-school/rhpyr04q43nmiy26hg5xelcagdsbwn2ulc.png)
![\[s_{\text{max}} = 20 * 10^(-6) * 10^((120 / 20))\]](https://img.qammunity.org/2024/formulas/physics/high-school/eai82x4dzn047tmryqcarfbpw143b4aiee.png)
Calculate
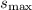 :
:
![\[s_{\text{max}} \approx 0.632 \, \text{m}\]](https://img.qammunity.org/2024/formulas/physics/high-school/ekrmv6j0i7fpaih5t0apbj2oldy2ifxnib.png)
The maximum displacement of the air molecules produced by the 8.0 Hz sound wave is approximately
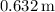 .
.
Next, to find the energy delivered to the wall by this wave, we can use the formula for the energy carried by a sound wave over an area:
![\[ \text{Energy} = \text{Intensity} * \text{Area} * \text{Time} \]](https://img.qammunity.org/2024/formulas/physics/high-school/btnbkbq1jpof6z5dzef1ap97g7q5uml0ub.png)
The intensity (I) of a sound wave is related to the sound pressure level
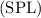 :
:
![\[ \text{Intensity} = I_0 * 10^{\left(\frac{\text{SPL}}{10}\right)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/vwwglnjxqbd9meh3sts8w1rhiu4ya99zmv.png)
Given:
Area (A) of the wall
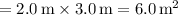
Time (t) = 1.0 minute = 60 seconds
First, let's find the intensity using the sound pressure level:
![\[ \text{Intensity} = I_0 * 10^{\left((120)/(10)\right)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/juvpo6r4anp9nqirrk6cj1i89qf3hc31wv.png)
![\[ \text{Intensity} = I_0 * 10^(12) \]](https://img.qammunity.org/2024/formulas/physics/high-school/ivfr651wlyw1a6xofdlhhboqe0reg2q7o2.png)
Since we're given the density of air, we can use the relationship between intensity, pressure, and density for a sound wave:
![\[ \text{Intensity} = (1)/(2) * \text{pressure}^2 * \text{velocity} \]](https://img.qammunity.org/2024/formulas/physics/high-school/ircz9ir2rmln0p0k6e7lt73on29amvvj4i.png)
![\[ \text{Pressure} = \sqrt{2 * \text{Intensity} * \text{density}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/s0ueu6g858faswue29dafhmwtztnbgvkc9.png)
Substituting the given values:
![\[ \text{Pressure} = \sqrt{2 * \text{Intensity} * \text{density}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/s0ueu6g858faswue29dafhmwtztnbgvkc9.png)
![\[ \text{Pressure} = \sqrt{2 * (I_0 * 10^(12)) * 1.2 \, \text{kg/m}^3} \]](https://img.qammunity.org/2024/formulas/physics/high-school/v249w4e00aow6gudbod2ynmlbrp0aeblj6.png)
Now, we can calculate the pressure and then find the energy delivered to the wall using the formula for energy.
Let's proceed with the calculations.
To find the pressure from the intensity of the sound wave:
![\[\text{Intensity} = I_0 * 10^(12)\]](https://img.qammunity.org/2024/formulas/physics/high-school/anq11jboe4smcv69ujfuan4vcevarjivsx.png)
Given that
 (standard reference intensity), substitute and calculate the intensity:
(standard reference intensity), substitute and calculate the intensity:
![\[\text{Intensity} = 20 * 10^(-6) * 10^(12)\]](https://img.qammunity.org/2024/formulas/physics/high-school/u8akt7mpq7wog8m8fkjmafssveu2sfqd6k.png)
![\[\text{Intensity} = 20000 \, \text{Pa}\]](https://img.qammunity.org/2024/formulas/physics/high-school/rqte52dkk5y79g6ewdve0wzgix5qi1jgyo.png)
Now, calculate the pressure using the intensity and air density:
![\[\text{Pressure} = \sqrt{2 * \text{Intensity} * \text{density}}\]](https://img.qammunity.org/2024/formulas/physics/high-school/b3hxjkpoirg3obqlr8ee718aj44gbnkhmy.png)
![\[\text{Pressure} = √(2 * 20000 * 1.2)\]](https://img.qammunity.org/2024/formulas/physics/high-school/nnlhxn6rbeu6vjailm67aatxmvgfx5g8y6.png)
![\[\text{Pressure} = √(48000)\]](https://img.qammunity.org/2024/formulas/physics/high-school/4ovmxsn205me5bkku28iri3ommyh1621xk.png)
![\[\text{Pressure} \approx 219.09 \, \text{Pa}\]](https://img.qammunity.org/2024/formulas/physics/high-school/anv75n84x8guexfsgy4sbb0h4bxeuh2hy5.png)
Next, calculate the energy delivered to the wall using the formula:
![\[\text{Energy} = \text{Intensity} * \text{Area} * \text{Time}\]](https://img.qammunity.org/2024/formulas/physics/high-school/v372odbyxlgz0inygjyiexf9cuqenuqvwc.png)
Given:
Area (A) of the wall
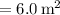
Time

![\[\text{Energy} = 20000 * 6.0 * 60\]](https://img.qammunity.org/2024/formulas/physics/high-school/tk36rxsc1swnfmjmqe90i8hv3k0ug10bab.png)
![\[\text{Energy} = 7200000 \, \text{J}\]](https://img.qammunity.org/2024/formulas/physics/high-school/b55j7sifa6v4txv1nn4f7cv9cuyot623mt.png)