The equilibrium value of
 is 5 moles. This means that at equilibrium, the system will have 5 moles of material in the liquid phase and 2 moles in the solid phase.
is 5 moles. This means that at equilibrium, the system will have 5 moles of material in the liquid phase and 2 moles in the solid phase.
At equilibrium, the chemical potentials of the two phases must be equal. This means that the free energy of transferring a mole of material from one phase to the other must be zero. Mathematically, we can express this as:

where:
 and
and
 are the number of moles in the liquid and solid phases, respectively
are the number of moles in the liquid and solid phases, respectively
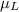 and
and
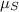 are the chemical potentials of the liquid and solid phases, respectively
are the chemical potentials of the liquid and solid phases, respectively
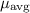 is the average chemical potential of the system
is the average chemical potential of the system
We are given that:
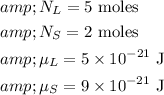
We can solve the equation for
 as follows:
as follows:

