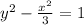Question

Find an equation for the hyperbola described. Graph the equation. Center at \( (0,0) \), focus at \( (0,2) \), vertex at \( (0,1) \)

Answer 1

Explanation:

Equation of an hyperbola is either

`\frac{(x - h) {}^(2) }{ {a}^(2) } - \frac{(y - k) {}^(2) }{ {b}^(2) } = 1`

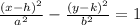
Or

`\frac{(y - k) {}^(2) }{ {a}^(2) } - \frac{( x - h) {}^(2) }{ {b}^(2) } = 1`

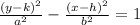
The variable

(h,k) is the center of hyperbola

Since (0,0) is the center, we can just use this equation

`\frac{ {y}^(2) }{ {b}^(2) } - \frac{ {x}^(2) }{ {a}^(2) } = 1`

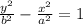
In this case, notice the focus and center both lie on the y axis, that means we have a vertical hyperbola so we will use the second equation for the hyperbola

The variable a is the semi major axis.(transverse axis)

The variable b is the semi minor axis (conjugate axis)

The vertex of a vertical hyperbola can be described as

(h,k+a),

The vertex is (0,0+1), so a is 1.

The focus of a vertical hyperbola can be described as

(h,k+c)

Where

`c = \sqrt{ {a}^(2) + {b}^(2) }`

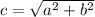
We know that c is 2 and a is 1.

`2 = \sqrt{1 + {b}^(2) }`

`3= {b}^(2)`

`√(3) = b`

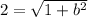
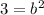
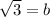
So our equation is

`{ {y}^(2) } - \frac{ {x}^(2) }{3} = 1`