Question

Find all z∈C such that cosh(z)+sinh(z)=−2022 or show that there are no such z∈C.

Answer 1

There are no real values z in
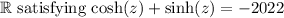`\( \mathbb{R} \) satisfying \( \cosh(z) + \sinh(z) = -2022 \)`. This is due to the nature of the equations involving hyperbolic trigonometric functions not reaching the required value in the real number set for the given equation.

Let's denote cos h(z) as x and sin h(z) as y. The equation cos h(z) + sin h(z) = -2022 can be rewritten using these substitutions as x + y = -2022.

From the trigonometric identity
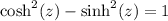`\( \cosh^2(z) - \sinh^2(z) = 1 \)`, we know that
`\( \cosh^2(z) = \sinh^2(z) + 1 \)`.

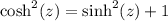Squaring the equation
`\( x + y = -2022 \) gives \( x^2 + 2xy + y^2 = 4088481 \)`.

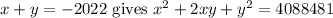Substituting
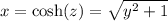`\( x = \cosh(z) = √(y^2 + 1) \)` into the equation yields:

`\[ (√(y^2 + 1))^2 + 2y√(y^2 + 1) + y^2 = 4088481 \]`

`\[ y^2 + 1 + 2y√(y^2 + 1) + y^2 = 4088481 \]`

`\[ 2y^2 + 2y√(y^2 + 1) = 4088480 \]`

`\[ 2y(y + √(y^2 + 1)) = 4088480 \]`

`\[ y(y + √(y^2 + 1)) = 2044240 \]`

This equation does not have real solutions since the product of two numbers (one being itself plus another) is always positive or zero. However, the right-hand side of the equation is a large positive number, meaning the left-hand side cannot reach that value with real numbers.

Therefore, there are no real values of z (or equivalently, x and y) that satisfy the equation cos h(z) + sin h(z) = -2022 in the set of real numbers
`(\( \mathbb{R} \))`.

Question:

Find all z∈R such that cos h(z)+sin h(z)=−2022 or show that there are no such z∈R.