Find the derivative of \tt \: tanh \: (x)/(2) Please help​

Question

Find the derivative of
`\tt \: tanh \: (x)/(2)`
Please help​

Answer 1

`\boxed{\tt (1)/(2)sech^2 ((x)/(2))}`

Explanation:

In order to find the derivative of
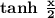`\bold{ tanh \:\:(x)/(2)}` , we can use the chain rule.

The chain rule states that the derivative of a composite function is the product of the derivative of the outer function and the derivative of the inner function.

In this case, the outer function is tanh(x) and the inner function is
`\tt (x)/(2)`

The derivative of tanh(x) is sech²(x), and the derivative of
`\tt (x)/(2)=(1)/(2)`.

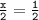So, the derivative of
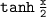`\tt tanh\:( x)/(2 )`is
`\tt sech^2((x)/(2)) *(1)/(2)`

Steps:

Let y =
`\bold{ tanh \:\:(x)/(2)}`

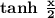
differentiating both sides with respect to x.

`\tt (dy)/(dx )= (d)/(dx) (tanh \:(x)/(2)).`

Using the chain rule, we have:

\frac{dy}{dx} =
`\tt sech^2((x)/(2)) *(1)/(2)`

Therefore, the derivative of
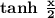`\bold{ tanh \:\:(x)/(2)}` is
`\boxed{\tt (1)/(2)sech^2 ((x)/(2))}`