Question

Urgent!! A polynomial function has zeros at 5, -6, and 9 as well as passes through the points P(2, m) and Q(-3, m + 30)

a) Find the values of the leading coefficient 'a' and 'm'.
b) Verify your answer by plugging in points P and Q into your function's equation

Answer 1

`a=(1)/(4)`

`m=42`

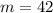
Explanation:

The zero of a polynomial is the x-value that makes the polynomial equal to zero when substituted into the polynomial expression.

If a polynomial function f(x) has zeros at 5, -6 and 9, then:

• f(5) = 0
• f(-6) = 0
• f(9) = 0

According to the Factor Theorem, if f(x) is a polynomial, and f(a) = 0, then (x - a) is a factor of f(x). Therefore, (x - 5), (x + 6) and (x - 9) are factors of the polynomial.

So we can write the factored polynomial as:

`f(x) = a(x-5)(x+6)(x-9)`

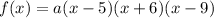
where "a" is the leading coefficient.

If the polynomial passes through points P(2, m) and Q(-3, m+30), then we can substitute these points into the polynomial f(x) and create two equations in terms of "a" and "m":

`\begin{aligned} (2,m) \implies a(2-5)(2+6)(2-9)&=m\\a(-3)(8)(-7)&=m\\168a&=m\end{aligned}`

`\begin{aligned} (-3, m+30) \implies a(-3-5)(-3+6)(-3-9)&=m+30\\a(-8)(3)(-12)&=m+30\\288a&=m+30\end{aligned}`

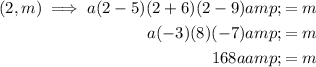
Substitute the first equation into the second equation and solve for "a":

`\begin{aligned}288a&=168a+30\\120a&=30\\a&=(1)/(4)\end{aligned}`

Substitute the found value of "a" into the first equation and solve for "m":

`\begin{aligned}168\cdot (1)/(4)&=m\\42&=m\\m&=42\end{aligned}`

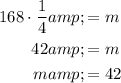
Therefore, the values of "a" and "m" are:

`\boxed{\boxed{a=(1)/(4)}}`
`\boxed{\boxed{\vphantom{\frac12}m=42}}`

`\hrulefill`

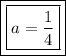
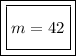
To verify the found values of "a" and "m", substitute the found value of "a" into the factored polynomial:

`f(x) = (1)/(4)(x-5)(x+6)(x-9)`

Substitute the found value of "m" into the expressions for points P and Q:

`P(2, m) =P(2,42)`

`Q(-3, m+30)=Q(-3,72)`

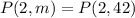
Now, substitute points P and Q into the polynomial, and verify that the y-value is true.

`\begin{aligned} (2,42) \implies (1)/(4)(2-5)(2+6)(2-9)&=42\\(1)/(4)(-3)(8)(-7)&=42\\42&=42\;\;\; \leftarrow \sf true\end{aligned}`

`\begin{aligned} (-3,72)\implies (1)/(4)(-3-5)(-3+6)(-3-9)&=72\\(1)/(4)(-8)(3)(-12)&=72\\72&=72 \;\;\;\leftarrow \sf true\end{aligned}`

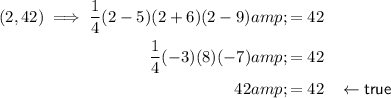
This verifies that a = 1/4 and m = 42.