Question

9) Find the value of 'b' such that the average rate of change over the interval x E [-2, -1] for the function f(x) = bx^2 + 3x is equal to 5

Answer 1

The value of b is
`\tt -(2)/(3)`

Explanation:

The average rate of change of a function f(x) over the interval [a, b] is given by:

`\boxed{\tt Average\:\: rate\:of\:change\: =((f(b) - f(a)) )/( (b - a))}`

In this case, the average rate of change is given to be 5, and the interval is [-2, -1]. So, we have

`\tt ((f(-1) - f(-2)) )/( (-1 - (-2)) )= 5`

`\tt f(-1) - f(-2) = 5`

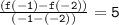
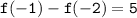
Let's evaluate f(-1) and f(-2) to find the value of 5 using the function
`\tt f(x) = bx^2 + 3x.`

f(-1) = b(-1)^2 + 3(-1) = b - 3

f(-2) = b(-2)^2 + 3(-2) = 4b - 6

Substituting these values into the equation f(-1) - f(-2) = 5, we get

b - 3 - (4b - 6) = 5

b-3-4b+6=5

-3b+3=5

-3b=5-3

`\tt -b=(2)/(3)`

`\tt b=-(2)/(3)`

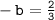
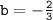
Therefore, the value of b such that the average rate of change over the interval x E [-2, -1] for the function
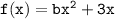`\tt f(x) = bx^2 + 3x` is equal to 5 is
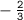`\tt - (2)/(3)`.

Answer 2

`b=-(2)/(3)`

Explanation:

To find the value of b such that the average rate of change over the interval [-2, -1] for the function f(x) = bx² + 3x is equal to 5, we can use the Average Rate of Change formula:

`\boxed{\begin{minipage}{6.3 cm}\underline{Average rate of change of function $f(x)$}\\\\$(f(b)-f(a))/(b-a)$\\\\over the interval $a \leq x \leq b$\\\end{minipage}}`

Given the interval is [-2, -1]:

• a = -2
• b = -1

Find f(a) and f(b) by substituting x = -2 and x = -1 into the given function f:

`\begin{aligned}f(a)=f(-2)&=b(-2)^2+3(-2)\\&=4b-6\end{aligned}`

`\begin{aligned}f(b)=f(-1)&=b(-1)^2+3(-1)\\&=b-3\end{aligned}`

Substitute the values of a, b, f(a) and f(b) into the average rate of change formula, and equate it to 5:

`\begin{aligned}(f(b)-f(a))/(b-a)&=5\\\\\implies ((b-3)-(4b-6))/(-1-(-2))&=5\end{aligned}`

Solve for b:

`\begin{aligned}((b-3)-(4b-6))/(-1-(-2))&=5\\\\(b-3-4b+6)/(-1+2)&=5\\\\(-3b+3)/(1)&=5\\\\-3b+3&=5\\\\-3b&=2\\\\b&=-(2)/(3)\end{aligned}`

Therefore, the value of b is -2/3.