Question

A polynomial function has zeros at 5, -6, and 9 as well as passes through the points P(2, m) and Q(-3, m + 30)

a) Find the values of the leading coefficient 'a' and 'm'.
b) Verify your answer by plugging in points P and Q into your function's equation

Answer 1

a. a=
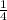`(1)/(4)` and m =42.

Explanation:

a. Since the polynomial function has zeros at 5, -6, and 9, its factored form is:

f(x) = a(x - 5)(x + 6)(x - 9)

The leading coefficient of this polynomial is not given, so we let it be represented by the variable a.

In order to find the value of m, we can plug in the point P(2, m) into the function's equation. This gives us the equation.

m = a(2 - 5)(2 + 6)(2 - 9)

Expanding the product on the right-hand side, we get

m = a(-3)(8)(-7)

So, we have the equation: m = 168a

To find the value of a, we can plug in the point Q(-3, m + 30) into the function's equation.

This gives us the equation

m + 30 = a(-3 - 5)(-3 + 6)(-3 - 9)

Expanding the product on the right-hand side, we get

m + 30 = a(-8)(3)(-12)

So, we have the equation: m + 30 = 288a

Now, we have two equations:

m = 168a .........[1]

m + 30 = 288a..[2]

To solve these equations, we can substitute the value of a in equation 2.

168a+30=288a

30=288a-168a

30=120a

`\tt a=(30)/(120)`

`\tt a=(1)/(4)`

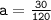
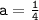
Now substitute value of a in equation 1.

`\tt m=168*(1)/(4)=42`

Therefore, the value of the leading coefficient a is
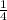`(1)/(4)` and m is 42.

`\hrulefill`

b. We can plug in the points P and Q into the function's equation, to verify our answer. The function's equation is

f(x) = a(x - 5)(x + 6)(x - 9)

Plugging in the point P(2, m) gives us

m = a(2 - 5)(2 + 6)(2 - 9)

`\tt m=(1)/(4)*(-3)*8*(-7)`

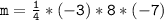
m=42

This is the same value of m that we found previously, so our answer is correct.

Plugging in the point Q(-3, m + 30) gives us

m + 30 = a(-3 - 5)(-3 + 6)(-3 - 9)

`m+30= (1)/(4)(-8)(3)(-12)`

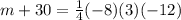
m+30= 72

m=72-30

m=42

This is the same value of m that we found previously, so our answer is correct.

Therefore, the leading coefficient a is
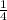`(1)/(4)` and the value of m is 42.