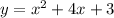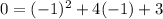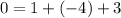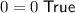Question

Let’s work through another example of this type of system together. Solve the system algebraically:

Answer 1

`\textsf{Step 2:} \quad 0=x^2+4x+3-\boxed{2}\:x-\boxed{2}`

`\textsf{Step 3:} \quad 0=x^2+\boxed{2}\:x+\boxed{1}`

`\begin{aligned}\textsf{Step 4:} \quad 0&=x^2+\boxed{2}\:x+\boxed{1}\\0&=\left(x+\boxed{1}\:\right)\left(x+\boxed{1}\:\right)\; \textsf{or}\\0&=(x+1)^2\\x&+1=0\\x&=\boxed{-1}\end{aligned}`

`\textsf{Step 6:}\quad\left(\:\boxed{-1, 0}\:\right)`

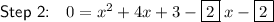
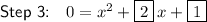
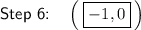
Explanation:

Given system of equations:

`\begin{cases}y=2x+2\\y=x^2+4x+3\end{cases}`

To solve the given system of equations algebraically, follow the given steps.

`\hrulefill`

Step 1

Set the two equations equal to one another (substitute for y).

(This step has been given to us).

`2x + 2 = x^2 + 4x + 3`

`\hrulefill`

Step 2

Set equal to 0 by subtracting 2x and 2 from both sides.

`2x + 2 -2x - 2 = x^2 + 4x + 3 - 2x - 2`

`0 = x^2 + 4x + 3 - 2x - 2`

`\hrulefill`

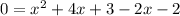
Step 3

Simplify/combine like terms.

`0 = x^2 + 4x + 3 - 2x - 2`

`0 = x^2 + 4x - 2x + 3 - 2`

`0 = x^2 + 2x + 1`

`\hrulefill`

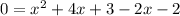
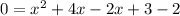
Step 4

Solve the quadratic equation by factoring:

`0 = x^2 + 2x + 1`

`0 = x^2 + x +x + 1`

`0 = x(x+1)+1(x + 1)`

`0 = (x+1)(x + 1)`

`0 = (x+1)^2`

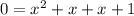
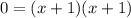
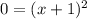
Therefore:

`x+1=0`

`x+1-1=0-1`

`x=-1`

`\hrulefill`

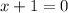
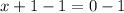
Step 5

Substitute the x value(s) into one of the equations and solve for y.

(This step has been given to us).

`y=2(-1)+2`

`y=-2+2`

`y=0`

`\hrulefill`

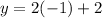
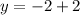
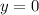
Step 6

Write the (x, y) point that solves the system.

`(-1, 0)`

`\hrulefill`

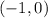
Step 7

Check point(s) in either original equation.

(This step has been given to us).

`y=x^2+4x+3`

`0=(-1)^2+4(-1)+3`

`0=1+(-4)+3`

`0=0\; \sf True`