Answer:
Equation of tangent:
Equation of normal:
Explanation:
Find the equation of tangents and normals to the following circle.x^2+y^2=40 at the point whose
Given:
ordinate is -6
abscissa is 2
Equation of circle:
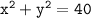
NowTangent at (2, -6):
since another coordinate is center which is in origin. so, we find the slope of the radius:
Slope of radius
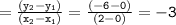
since radius is perpendicular to tangent, m2=-1/m1
The slope of the tangent =
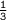
The equation of the tangent at (2, -6) is:
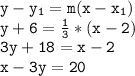
Therefore, the equations of the tangents to the circle x^2 + y^2 = 40 at the point (2, -6) are:
ii. normal is parallel to the x-axis
We need to find the slope of the tangent at the given point and then take the negative reciprocal of that slope to get the normal's slope to find the normal's equation to the circle parallel to the x-axis.
The slope of the tangent at (2, -6) is
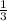 (we calculated this earlier).
(we calculated this earlier).
The slope of the normal = -1 / slope of the tangent =
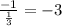
The equation of the normal is simply the equation of the horizontal line passing through the point (2, -6):
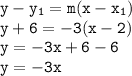
Therefore, the equation of the normal to the circle
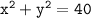 at the point (2, 6) parallel to the x-axis is
at the point (2, 6) parallel to the x-axis is