Question

Find the standard deviation of 3x,3x-1, and 3x+1

Answer 1

The standard deviation of 3x,3x-1, and 3x+1 is
`\sqrt{(5)/(27)}`

To find the standard deviation of 3x, 3x-1, and 3x+1, we have to,

• Find the mean of the set of numbers

• Subtract the mean from each number and square the result

• Then find the mean of the squared differences to get the standard deviation.

Find the mean,

Mean=

`((3x + (3x - 1) + (3x + 1)))/(3)\\\\(9x-1)/(3)\\\\(3x-1)/(3)`

Subtracting the mean and squaring,

`(3x - (3x-1)/(3))^2 =((1)/(3))^2=(1)/(9)\\\\(3x-1)-(\frac {3x-1}{3})^2=0\\\\(3x+1-((3x-1)/(3))^2= (4)/(9)`

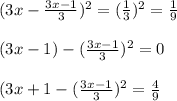
Now, we find the mean of the above terms,

`((1)/(9)+0+(4)/(9))/(3)=(5)/(9*3)=(5)/(27)`

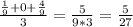
Now, taking the square root of the above result we get the standard deviation,

So, Standard deviation =
`\sqrt{(5)/(27)}`

Therefore, the standard deviation of the numbers 3x, 3x-1, and 3x+1 is
`\sqrt{(5)/(27)}`

To learn more about standard deviation: