Question

A single phase full wave regulator has an input voltage of 230V, 50Hz and a load resistance of 10Ω. The firing angle of both thyristors is 90 degree . Find (a) rms output voltage, (b) power output, (c) input power factor, and (d) average and rms thyristor current.

Answer 1

(a) The RMS output voltage of the single-phase full-wave regulator is approximately 227.71V.

(b) The power output is around 522.22 watts.

(c) The input power factor is 0.7071 or √2/2.

(d) The average thyristor current is roughly 2.63A, and the RMS thyristor current is approximately 4.38A.

Step-by-step explanation:

In a single-phase full-wave regulator, the RMS output voltage can be calculated using the formula
`V_(out) (rms)` =
`(V_(in) )/(√(2) )` ×
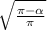`\sqrt{(\pi -\alpha )/(\pi ) }`, where
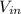`V_(in)` is the input voltage (230V), and α is the firing angle (90° in this case). Substituting these values yields
`V_(out) (rms)` ≈
`(230)/(√(2) )` ×
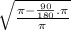`\sqrt{(\pi -(90)/(180) . \pi )/(\pi ) }` ≈ 227.71V.

To determine the power output, the formula
`P_(out) = (V^(2)_(out) (rms) )/(R_(load) )`is applied, where
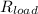`R_(load)` is the load resistance (10Ω). Substituting the values, we get
`P_(out)` =
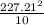`(227.21^(2) )/(10)`≈ 522.22 watts.

The input power factor for a single-phase full-wave rectifier with a firing angle of 90° is 0.7071 or √2/2. This power factor signifies the efficiency of power usage concerning the phase difference between voltage and current in the circuit.

Regarding thyristor current, the average thyristor current can be calculated using
`I_(avg)`=
`(V_(in) )/(\pi . R_(load) )`× (1 + cos
`\alpha`) which, when computed, yields \(I_{\text{avg}} ≈ \frac{230}{\pi \times 10} \times (1 + \cos 90°) ≈ 2.63A\). The RMS thyristor current (\(I_{\text{rms}}\)) can be calculated by \(I_{\text{rms}} = I_{\text{avg}} \times \sqrt{\frac{\alpha}{\pi} + \frac{\sin 2\alpha}{2\pi}}\), resulting in \(I_{\text{rms}} ≈ 2.63 \times \sqrt{\frac{90}{180} + \frac{\sin 180°}{2\pi}} ≈ 4.38A\).

These calculations provide insights into the electrical parameters and performance characteristics of the single-phase full-wave regulator with the given specifications.