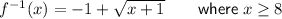Question

Find the inverse function of f(x)=x^2+2x where x≥2. Then, find the domain of f^-1(x)

Answer 1

`f^(-1)(x)=-1 + √(x+1) \qquad\textsf{where}\; x\geq 8`

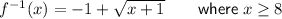
Explanation:

Given function:

`f(x)=x^2+2x`

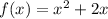
The domain of the given function is restricted: x ≥ 2

Therefore, the range of the given function is also restricted: f(x) ≥ 8

To find the inverse of a function, swap x and y:

`x=y^2+2y`

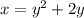
Subtract x from both sides:

`y^2+2y-x=0`

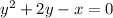
Isolate y by using the quadratic formula:

`y=(-b \pm √(b^2-4ac))/(2a),\;\;\textsf{where}\;ay^2+by+c=0`

Therefore, a = 1, b = 2, c = -x:

`y=(-2 \pm √(2^2-4(1)(-x)))/(2(1))`

`y=(-2 \pm √(4+4x))/(2)`

`y=(-2 \pm √(4(1+x)))/(2)`

`y=(-2 \pm √(4)√(1+x))/(2)`

`y=(-2 \pm 2√(1+x))/(2)`

`y=-1 \pm √(x+1)`

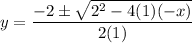
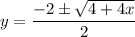
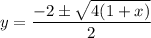
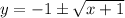
Replace y with f⁻¹(x):

`f^(-1)(x)=-1 \pm √(x+1)`

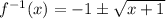
The domain of the inverse of a function is the same as the range of the original function. Given the range of the original function is f(x) ≥ 8, then the domain of the inverse function is restricted to x ≥ 8.

`\textsf{When\;\;$x \geq 8 \implies f^(-1)(x) = -1 - √(x + 1) \leq -4$}`

`\textsf{When\;\;$x \geq 8 \implies f^(-1)(x) = -1 +√(x + 1) \geq 2$}`

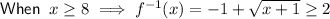
The range of the inverse of a function is the same as the domain of the original function. Given the domain of the original function is x ≥ 2, then the range of the inverse function is restricted to x ≥ 2.

Therefore, as the range of the inverse function is f⁻¹(x) ≥ 2, the inverse of function f(x) is:

`f^(-1)(x)=-1 + √(x+1) \qquad\textsf{where}\; x\geq 8`